Tutorial 5 Evaluating hypotheses regarding the shape of activity curves
Diel activity patterns are often described or classified as either:
- unimodal: the species is mostly active during a restricted portion of the 24-hour cycle, and not (or almost not) active in the remaining time. The activity curve is characterized by only one peak, and it is typical of species that are either diurnal or nocturnal.
- bimodal: the species is mostly active during two specific times of the 24-hour cycle, often corresponding to sunrise and sunset (i.e. crepuscular species) and inactive (or mostly inactive) during the rest of the time. The activity curve is characterized by having two peaks.
- cathemeral (non-modal): the species is equally active throughout the 24-hour cycle and the activity curve approximates a flat line.
Here, we build and compare trigonometric hierarchical models representing these three different diel activity patterns. To reiterate, we use independent camera-trap records of coyotes (Canis latrans) collected between 2016 and 2018 at 100 locations in Northern Minnesota, USA, (Iannarilli et al. 2021), with the data organized as described in the previous Tutorial 4.
# Load libraries
set.seed(129)
library(dplyr)
library(lubridate)
library(GLMMadaptive)
library(lmtest)
library(ggpubr)
head(occasions_cbind)## # A tibble: 6 × 4
## # Groups: Site [1]
## Site Time success failure
## <fct> <int> <dbl> <dbl>
## 1 10A 0 0 259
## 2 10A 1 0 259
## 3 10A 2 0 259
## 4 10A 3 0 259
## 5 10A 4 0 259
## 6 10A 5 0 259We start by fitting a model that describes a unimodal activity pattern. This structure includes only the first of the two cosine terms in equation 1 (which translates in the first and second terms of equation 2), and a random intercept and a random slope as described in Tutorial 3.
# Unimodal
unimodal <- mixed_model(fixed = cbind(success, failure) ~ cos(2*pi*Time/24) + sin(2*pi*Time/24),
random = ~ cos(2*pi*Time/24) + sin(2*pi*Time/24) || Site,
family = binomial(),
data = occasions_cbind
)
summary(unimodal)##
## Call:
## mixed_model(fixed = cbind(success, failure) ~ cos(2 * pi * Time/24) +
## sin(2 * pi * Time/24), random = ~cos(2 * pi * Time/24) +
## sin(2 * pi * Time/24) || Site, data = occasions_cbind, family = binomial())
##
## Data Descriptives:
## Number of Observations: 2400
## Number of Groups: 100
##
## Model:
## family: binomial
## link: logit
##
## Fit statistics:
## log.Lik AIC BIC
## -660.5908 1333.182 1348.813
##
## Random effects covariance matrix:
## StdDev
## (Intercept) 1.4853
## cos(2 * pi * Time/24) 0.5347
## sin(2 * pi * Time/24) 0.5315
##
## Fixed effects:
## Estimate Std.Err z-value p-value
## (Intercept) -9.0125 0.2182 -41.3085 < 1e-04
## cos(2 * pi * Time/24) 0.5754 0.1334 4.3133 < 1e-04
## sin(2 * pi * Time/24) 0.2232 0.1306 1.7091 0.08743
##
## Integration:
## method: adaptive Gauss-Hermite quadrature rule
## quadrature points: 7
##
## Optimization:
## method: hybrid EM and quasi-Newton
## converged: TRUETo code for a bimodal activity pattern, we extend the model structure above by also including the second cosine term in equation 1 (i.e. third and forth terms in equation 2).
# Bimodal
bimodal <- mixed_model(fixed = cbind(success, failure) ~ cos(2*pi*Time/24) + sin(2*pi*Time/24)+
cos(2*pi*Time/12) + sin(2*pi*Time/12),
random = ~ cos(2*pi*Time/24) + sin(2*pi*Time/24)+
cos(2*pi*Time/12) + sin(2*pi*Time/12) || Site,
family = binomial(),
data = occasions_cbind
)
summary(bimodal)##
## Call:
## mixed_model(fixed = cbind(success, failure) ~ cos(2 * pi * Time/24) +
## sin(2 * pi * Time/24) + cos(2 * pi * Time/12) + sin(2 * pi *
## Time/12), random = ~cos(2 * pi * Time/24) + sin(2 * pi *
## Time/24) + cos(2 * pi * Time/12) + sin(2 * pi * Time/12) ||
## Site, data = occasions_cbind, family = binomial())
##
## Data Descriptives:
## Number of Observations: 2400
## Number of Groups: 100
##
## Model:
## family: binomial
## link: logit
##
## Fit statistics:
## log.Lik AIC BIC
## -654.8336 1329.667 1355.719
##
## Random effects covariance matrix:
## StdDev
## (Intercept) 1.4885
## cos(2 * pi * Time/24) 0.6659
## sin(2 * pi * Time/24) 0.4075
## cos(2 * pi * Time/12) 0.1727
## sin(2 * pi * Time/12) 0.1757
##
## Fixed effects:
## Estimate Std.Err z-value p-value
## (Intercept) -9.0816 0.2228 -40.7584 < 1e-04
## cos(2 * pi * Time/24) 0.6865 0.1567 4.3824 < 1e-04
## sin(2 * pi * Time/24) 0.2897 0.1221 2.3722 0.017683
## cos(2 * pi * Time/12) -0.2782 0.1195 -2.3277 0.019927
## sin(2 * pi * Time/12) -0.2451 0.1055 -2.3225 0.020205
##
## Integration:
## method: adaptive Gauss-Hermite quadrature rule
## quadrature points: 7
##
## Optimization:
## method: hybrid EM and quasi-Newton
## converged: TRUEFinally, we use a model without any cosine term to describe a cathemeral activity patterns. We include a random intercept but cannot include a random slope due the structure of model itself.
null_mod <- mixed_model(fixed = cbind(success, failure) ~ 1,
random = ~ 1 | Site,
family = binomial(),
data = occasions_cbind
)
summary(null_mod)##
## Call:
## mixed_model(fixed = cbind(success, failure) ~ 1, random = ~1 |
## Site, data = occasions_cbind, family = binomial())
##
## Data Descriptives:
## Number of Observations: 2400
## Number of Groups: 100
##
## Model:
## family: binomial
## link: logit
##
## Fit statistics:
## log.Lik AIC BIC
## -697.7788 1399.558 1404.768
##
## Random effects covariance matrix:
## StdDev
## (Intercept) 1.508908
##
## Fixed effects:
## Estimate Std.Err z-value p-value
## (Intercept) -8.7938 0.2179 -40.361 < 1e-04
##
## Integration:
## method: adaptive Gauss-Hermite quadrature rule
## quadrature points: 11
##
## Optimization:
## method: EM
## converged: TRUEModel selection. We can now proceed to compare the different model structures and associated hypotheses. We can do this using the Akaike Information Criterion (AIC; Burnham and Anderson (2002)).
## df AIC
## null_mod 2 1399.558
## unimodal 6 1333.182
## bimodal 10 1329.667We can also compare the models using a Likelihood Ratio Test (LRT).
## Likelihood ratio test
##
## Model 1: cbind(success, failure) ~ 1
## Model 2: cbind(success, failure) ~ cos(2 * pi * Time/24) + sin(2 * pi *
## Time/24)
## Model 3: cbind(success, failure) ~ cos(2 * pi * Time/24) + sin(2 * pi *
## Time/24) + cos(2 * pi * Time/12) + sin(2 * pi * Time/12)
## #Df LogLik Df Chisq Pr(>Chisq)
## 1 2 -697.78
## 2 6 -660.59 4 74.376 2.7e-15 ***
## 3 10 -654.83 4 11.514 0.02135 *
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1Both comparisons suggest that the bimodal pattern is the most supported model among those compared. We can, thus, conclude that coyotes have a bimodal activity pattern.
We can also visually compare predicted activity curves based on these models. As in other examples, we first use the function GLMMadaptive::effectPlotData to predict the activity curves throughout the 24-hour cycle and then use ggplot to plot the results.
# build a new dataset
newdat <- with(occasions_cbind,
expand.grid(Time = seq(min(Time), max(Time), length.out = 24)
)
)
# obtain the estimated activity curves
predict_unimodal <- effectPlotData(unimodal, newdat, marginal = FALSE) %>%
mutate(Model = "Unimodal")
predict_bimodal <- effectPlotData(bimodal, newdat, marginal = FALSE) %>%
mutate(Model = "Bimodal")
predict_cathemeral <- effectPlotData(null_mod, newdat, marginal = FALSE) %>%
mutate(Model = "Cathemeral")# join and plot results
pl_shapes <- rbind(predict_unimodal, predict_bimodal, predict_cathemeral) %>%
ggplot(., aes(x = Time, y = plogis(pred), group = Model, fill = Model)) +
geom_line(aes(colour = Model)) +
geom_ribbon(aes(ymin = plogis(low), ymax = plogis(upp), colour = NULL), alpha = 0.3) +
labs(x = "Time of Day (Hour)", y = "Predicted Activity Pattern \n (probability)")+
theme_minimal()+
theme(legend.position = "top",
legend.title = element_blank(),
legend.text = element_text(size=10,face="bold"),
legend.margin=margin(0,0,0,0),
legend.box.margin=margin(-5,-10,-10,-10),
plot.title = element_blank(),
axis.line = element_line(colour = 'black', linetype = 'solid'),
axis.ticks = element_line(colour = 'black', linetype = 'solid'),
axis.title = element_text(size=9,face="bold"),
panel.grid.minor.y = element_blank(),
panel.grid.major.y = element_blank(),
panel.grid.major.x = element_line(colour = 'lightgrey', linetype = 'dashed', linewidth=0.5),
panel.grid.minor.x = element_blank(),
strip.text = element_text(size = 9, colour = "black", face = "bold", hjust = 0)
) +
#panel.grid.minor.x = element_line(colour='deepskyblue4', linetype = 'dotted', size=0.35))+
scale_x_continuous(breaks=seq(0,23,length.out=7), labels=seq(0,24,4))
pl_shapes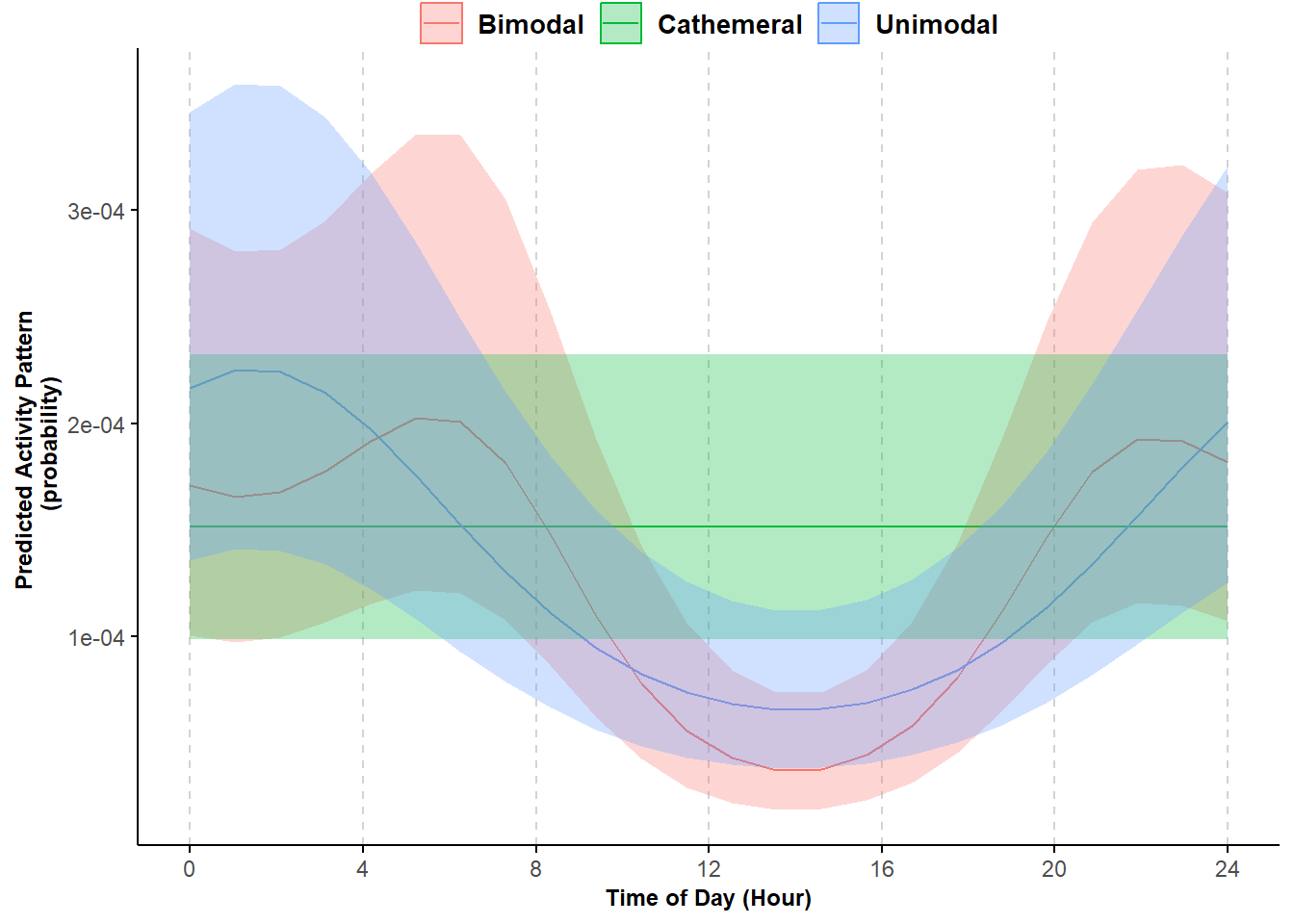
Figure 5.1: Predicted probability of activity by three hypotheses: unimodal, bimodal, and cathemeral; shading represented 95% confidence intervals.
# save plot
ggsave(plot = pl_shapes, filename = "ms_figures/Fig2_Uni_vs_Bim_comparison.jpg", device = "jpeg", units = "cm", width = 12, height = 10, dpi = 600)We can test other hypotheses related to the shape of the activity curve (e.g., three or more peaks) for our target species by simply adding additional cosine terms to the model structure and then comparing the different structures using AIC or LRT. However, going beyond two peaks might be computationally challenging, especially when a random slope is included. In these cases, one might need to consider reducing model complexity by only including a random intercept.