Tutorial 7 Temporal partitioning
Another common question related to activity patterns often asked by ecologists is whether a species changes its activity due to the co-occurrence of another species. In this Tutorial, we illustrate how hierarchical models can be used to also address this set of questions.
As an example, we analyze temporal partitioning between coyotes and wolves (Canis lupus). We format the data as usual.
# Load libraries
rm(list = ls())
set.seed(129)
library(dplyr)
library(lubridate)
library(GLMMadaptive)
library(ggpubr)
library(mgcv)
library(forcats)# Load data: Coyote/Wolf Species interactions
dat <- read.csv("data_input/species_records.csv", as.is = TRUE) %>%
filter(c(Species == "Coyote" | Species == "Wolf")) %>% droplevels() %>%
mutate(DateTimeOriginal = ymd_hm(DateTimeOriginal))
cov <- read.csv("data_input/CameraTrapProject_CT_data_for_analysis_MASTER.csv", as.is = TRUE) %>%
select(c(Session, Site, Date_setup, Date_retr, Problem1_from, Problem1_to)) %>%
mutate(Date_setup = mdy(Date_setup),
Date_retr = mdy(Date_retr),
Problem1_from = mdy(Problem1_from),
Problem1_to = mdy(Problem1_to)
) However, before organizing the data using the cbind(success, failure) approach we need to include the additional information on whether the other species was also detected at least once at a certain site during a sampling session. We thus create two lists of site X session (hereafter, site-session) in which either wolves or coyotes have been encountered and then look at the overlap between these two lists.
# Where both species were detected at the same site during a session?
# List sites with at least a detection on a given session
site_Co <- dat %>% filter(Species == "Coyote") %>% group_by(Session, Station) %>%
summarize(n = n()) ## `summarise()` has grouped output by 'Session'. You can override using the `.groups` argument.## `summarise()` has grouped output by 'Session'. You can override using the `.groups` argument.site <- semi_join(site_Co, site_Wo, by = c("Session", "Station")) %>%
mutate(Sess_site = paste(Session, Station, sep = "_"))Wolves and coyotes have been detected at 191 and 104 site-sessions, respectively, and 47 times both species occurred at the same site-session.
# Add binary variable for presence of other species
dat$oth_sp <- NA
for(i in 1:nrow(dat)){
dat$oth_sp[i] <- ifelse(paste(dat$Session[i], dat$Station[i], sep = "_") %in% site$Sess_site, 1,0)
}
table(dat$Species, dat$oth_sp)##
## 0 1
## Coyote 3209 1747
## Wolf 8148 2248For each species (e.g., coyote), we used a dummy variable called oth_sp to describe whether the other species (e.g., wolf) was photographed at least once (oth_sp = 1; 0 otherwise) at the same site during a specific site-session. This resulted in 1747 and 3209 records of coyotes at site-sessions where wolves were and were not recorded, and 2248 and 8148 records of wolves at site-sessions where coyotes were and were not recorded. With this additional piece of information, we can proceed with formatting the data (i.e. counting the number of successes and failures for each grouping). We build a dataframe to store the encounter/nonencounter information for each species.
# Prepare data for model-based methods
# Merge time of deployment and retrieval + problems
site_Co2 <- cov
site_Co2$end <- ymd("2000-01-01")
for(i in 1:nrow(site_Co2)){
site_Co2$end[i] <- min(site_Co2$Date_retr[i],
site_Co2$Problem1_from[i],
na.rm = TRUE
)
}
# Create dataframe to store captures
occasions_Co <- vector("list", length = nrow(site_Co2))
for(i in 1:nrow(site_Co2)){
occasions_Co[[i]] <- data.frame(Session = site_Co2$Session[i],
site = site_Co2$Site[i],
start = seq(from = ymd_hms(paste(site_Co2$Date_setup[i], "00:00:00", sep = " ")),
to = ymd_hms(paste(site_Co2$end[i], "23:59:59", sep = " ")), by = '60 min')
) %>%
mutate(end = c(start[2:length(start)],
start[length(start)]+minutes(60)
)
)
}
occasions_Co <- do.call(rbind.data.frame, occasions_Co)
occasions_Co$capt <- 0
occasions_Wo <- occasions_CoThen, we populate these dataframes with the information recorded for coyotes and wolves, respectively. We start with coyotes.
# Coyote data:
# Store captures
dat_Co <- dat %>% filter(Species == "Coyote")
for(i in 1:nrow(dat_Co)){
occasions_Co[occasions_Co$Session == as.character(dat_Co$Session[i]) &
occasions_Co$site == as.character(dat_Co$Station[i]) &
occasions_Co$start <= dat_Co$DateTimeOriginal[i] &
occasions_Co$end > dat_Co$DateTimeOriginal[i], "capt"] <- 1
}
# Format data
occasions_Co$Time <- hour(occasions_Co$start)
occasions_Co$oth_sp <- NA
for(i in 1:nrow(occasions_Co)){
occasions_Co$oth_sp[i] <- ifelse(paste(occasions_Co$Session[i], occasions_Co$site[i], sep = "_") %in% site$Sess_site, 1,0)
}
table(occasions_Co$oth_sp, occasions_Co$capt)##
## 0 1
## 0 514127 121
## 1 56798 130occasions_Co$site <- as.factor(occasions_Co$site)
occasions_Co$oth_sp <- as.factor(occasions_Co$oth_sp)
# format data for cbind(success, failure)
occasions_Co_cbind <- occasions_Co %>%
group_by(site, Time, oth_sp) %>%
summarize(success = sum(capt),
failure = n() - success)## `summarise()` has grouped output by 'site', 'Time'. You can override using the `.groups` argument.We had 130 hourly intervals (out of 56 928) and 121 hourly intervals (out of 514 248) in which coyotes were recorded at a site-session where wolves were and were not photographed.
We repeat the same steps for wolves.
# Store captures
dat_Wo <- dat %>% filter(Species == "Wolf")
for(i in 1:nrow(dat_Wo)){
occasions_Wo[occasions_Wo$Session == as.character(dat_Wo$Session[i]) &
occasions_Wo$site == as.character(dat_Wo$Station[i]) &
occasions_Wo$start <= dat_Wo$DateTimeOriginal[i] &
occasions_Wo$end > dat_Wo$DateTimeOriginal[i], "capt"] <- 1
}
# Format data
occasions_Wo$Time <- hour(occasions_Wo$start)
occasions_Wo$oth_sp <- NA
for(i in 1:nrow(occasions_Wo)){
occasions_Wo$oth_sp[i] <- ifelse(paste(occasions_Wo$Session[i], occasions_Wo$site[i], sep = "_") %in% site$Sess_site, 1,0)
}
table(occasions_Wo$oth_sp, occasions_Wo$capt)##
## 0 1
## 0 513894 354
## 1 56747 181occasions_Wo$site <- as.factor(occasions_Wo$site)
occasions_Wo$oth_sp <- as.factor(occasions_Wo$oth_sp)
# format data for cbind(success, failure)
occasions_Wo_cbind <- occasions_Wo %>%
group_by(site, Time, oth_sp) %>%
summarize(success = sum(capt),
failure = n() - success)## `summarise()` has grouped output by 'site', 'Time'. You can override using the `.groups` argument.For this species, we had 181 (out of 56 928) and 354 (out of 514 248) hourly intervals with at least 1 record of wolves at site-sessions in which coyotes were and were not recorded.
We now proceed to fit a model to the data for each species. For convenience, we run a trigonometric random intercept-only model, but more complex trigonometric GLMMs or cyclic cubic spline HGAMs could be considered.
# run model: coyote
mod_trig_Co <- mixed_model(fixed = cbind(success, failure) ~ cos(2*pi*Time/24)*oth_sp + sin(2*pi*Time/24)*oth_sp +
cos(2*pi*Time/12)*oth_sp + sin(2*pi*Time/12)*oth_sp,
random = ~ 1 | site,
family = binomial(),
data = occasions_Co_cbind,
iter_EM = 0
)
summary(mod_trig_Co)##
## Call:
## mixed_model(fixed = cbind(success, failure) ~ cos(2 * pi * Time/24) *
## oth_sp + sin(2 * pi * Time/24) * oth_sp + cos(2 * pi * Time/12) *
## oth_sp + sin(2 * pi * Time/12) * oth_sp, random = ~1 | site,
## data = occasions_Co_cbind, family = binomial(), iter_EM = 0)
##
## Data Descriptives:
## Number of Observations: 3168
## Number of Groups: 100
##
## Model:
## family: binomial
## link: logit
##
## Fit statistics:
## log.Lik AIC BIC
## -743.6756 1509.351 1538.008
##
## Random effects covariance matrix:
## StdDev
## (Intercept) 1.164095
##
## Fixed effects:
## Estimate Std.Err z-value p-value
## (Intercept) -9.0237 0.1935 -46.6262 < 1e-04
## cos(2 * pi * Time/24) 0.6432 0.1617 3.9778 < 1e-04
## oth_sp1 1.4042 0.1932 7.2670 < 1e-04
## sin(2 * pi * Time/24) 0.3302 0.1322 2.4974 0.012512
## cos(2 * pi * Time/12) -0.3449 0.1389 -2.4830 0.013030
## sin(2 * pi * Time/12) -0.3411 0.1392 -2.4502 0.014279
## cos(2 * pi * Time/24):oth_sp1 0.1993 0.2248 0.8866 0.375297
## oth_sp1:sin(2 * pi * Time/24) 0.0174 0.1953 0.0892 0.928941
## oth_sp1:cos(2 * pi * Time/12) 0.3083 0.1946 1.5840 0.113191
## oth_sp1:sin(2 * pi * Time/12) 0.1930 0.1954 0.9876 0.323334
##
## Integration:
## method: adaptive Gauss-Hermite quadrature rule
## quadrature points: 11
##
## Optimization:
## method: quasi-Newton
## converged: TRUE# run model: wolf
mod_trig_Wo <- mixed_model(fixed = cbind(success, failure) ~ cos(2*pi*Time/24)*oth_sp + sin(2*pi*Time/24)*oth_sp +
cos(2*pi*Time/12)*oth_sp + sin(2*pi*Time/12)*oth_sp,
random = ~ 1 | site,
family = binomial(),
data = occasions_Wo_cbind,
iter_EM = 0
)
summary(mod_trig_Wo)##
## Call:
## mixed_model(fixed = cbind(success, failure) ~ cos(2 * pi * Time/24) *
## oth_sp + sin(2 * pi * Time/24) * oth_sp + cos(2 * pi * Time/12) *
## oth_sp + sin(2 * pi * Time/12) * oth_sp, random = ~1 | site,
## data = occasions_Wo_cbind, family = binomial(), iter_EM = 0)
##
## Data Descriptives:
## Number of Observations: 3168
## Number of Groups: 100
##
## Model:
## family: binomial
## link: logit
##
## Fit statistics:
## log.Lik AIC BIC
## -1275.273 2572.546 2601.203
##
## Random effects covariance matrix:
## StdDev
## (Intercept) 1.134112
##
## Fixed effects:
## Estimate Std.Err z-value p-value
## (Intercept) -7.8886 0.1439 -54.8261 < 1e-04
## cos(2 * pi * Time/24) 0.5082 0.0880 5.7740 < 1e-04
## oth_sp1 0.4711 0.1457 3.2344 0.00121891
## sin(2 * pi * Time/24) 0.3586 0.0783 4.5796 < 1e-04
## cos(2 * pi * Time/12) -0.2094 0.0791 -2.6452 0.00816464
## sin(2 * pi * Time/12) -0.3083 0.0800 -3.8520 0.00011716
## cos(2 * pi * Time/24):oth_sp1 0.1295 0.1457 0.8893 0.37385895
## oth_sp1:sin(2 * pi * Time/24) -0.1112 0.1473 -0.7547 0.45045328
## oth_sp1:cos(2 * pi * Time/12) 0.4407 0.1379 3.1956 0.00139527
## oth_sp1:sin(2 * pi * Time/12) -0.0862 0.1405 -0.6133 0.53966172
##
## Integration:
## method: adaptive Gauss-Hermite quadrature rule
## quadrature points: 11
##
## Optimization:
## method: quasi-Newton
## converged: TRUEWe now plot the results for both coyotes and wolves in the presence and absence of the other species. We focus on estimating marginal mean activity patterns because our aim is to compare between two groups that differ in their characteristics (i.e. site-sessions with and without the other species). The only change to the code required to obtain the marginal means is to set the argument marginal in the effectPlotData function equal to TRUE (see Tutorial 8 for more on conditional and marginal mean activity patterns).
# coyote
newdat <- with(occasions_Co_cbind, expand.grid(Time = seq(min(Time), 24, length.out = 48),
oth_sp = as.factor(c(0,1))
)
)
cond_eff_Co <- effectPlotData(mod_trig_Co, newdat, marginal = TRUE)
cond_eff_Co$Species <- "Coyote"
# wolf
newdat <- with(occasions_Wo_cbind, expand.grid(Time = seq(min(Time), 24, length.out = 48),
oth_sp = as.factor(c(0,1))
)
)
cond_eff_Wo <- effectPlotData(mod_trig_Wo, newdat, marginal = TRUE)
cond_eff_Wo$Species <- "Wolf"
cond_eff <- rbind(cond_eff_Co, cond_eff_Wo) %>%
mutate(oth_sp_labels = fct_recode(oth_sp, "Without the other species" = "0", "With the other species" = "1"))(pl_trig <- ggplot(cond_eff, aes(Time, plogis(pred), color=Species, group=Species)) +
geom_ribbon(aes(ymin=plogis(low), ymax=plogis(upp), fill=Species), alpha=0.5, linewidth = 0.25) +
geom_line(size=1) +
labs(x = "Time of Day (Hour)", y = "Predicted Activity Pattern \n (probability)", title = "A: trigonometric GLMMs")+
scale_color_manual(values = c("#E69F00", "#0072B2")) +
scale_fill_manual(values = c("#E69F00", "#0072B2")) +
theme_minimal()+
theme(legend.position = "right",
legend.title = element_text(size=10,face="bold"),
plot.title = element_blank(),
axis.line = element_line(colour = 'black', linetype = 'solid'),
axis.ticks = element_line(colour = 'black', linetype = 'solid'),
axis.title = element_text(size=9,face="bold"),
panel.grid.minor.y = element_blank(),
panel.grid.major.y = element_blank(),
panel.grid.major.x = element_line(colour = 'lightgrey', linetype = 'dashed', linewidth=0.5),
panel.grid.minor.x = element_blank(),
strip.text = element_text(face = "bold")
) +
scale_x_continuous(breaks=seq(0,24,4), labels=seq(0,24,4)) +
facet_wrap(~oth_sp_labels, scales = "fixed")
)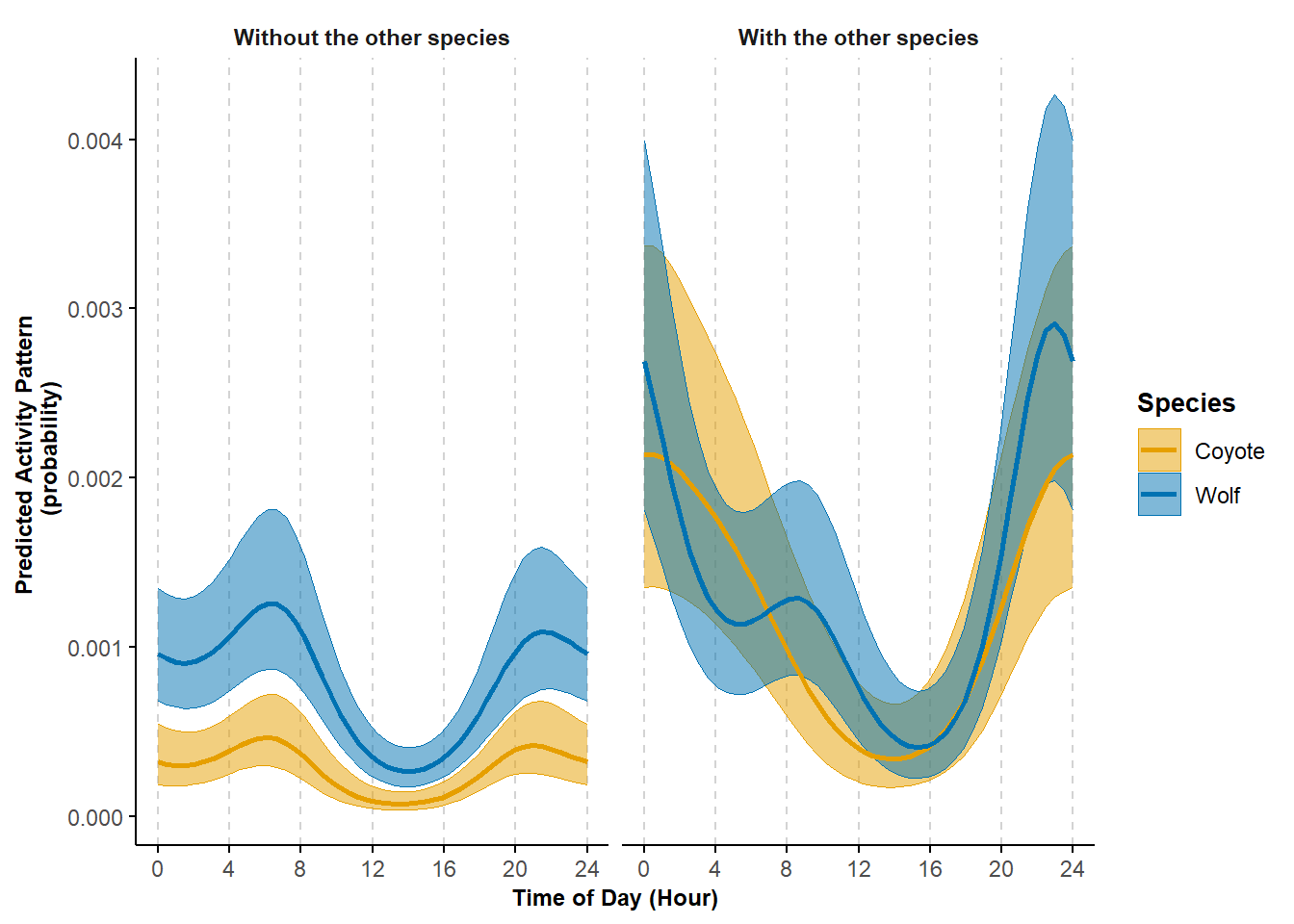
Figure 7.1: Predicted probability of activity by coyote and wolf and depending on each others presence or absence; shading corresponds to 95% confidence intervals.
ggsave(plot = pl_trig, filename = "ms_figures/Fig5_Coyote_Wolf_patterns.jpg", device = "jpeg", units = "cm", width = 24, height = 10, dpi = 600)This figure is presented in Iannarilli et al. (2024) as Figure 5; there, we offer additional discussion regarding the estimated activity curves.
Next, we consider a cyclic cubic spline HGAM (without a site-specific smoother) for each species, which we compare to the trigonometric GLMM below.
# Cyclic cubic splines ('random intercept-only')
# Coyote
mod_cycl_Co <- bam(cbind(success, failure) ~ s(Time, bs = "cc", k = 12, by = oth_sp, m = 1) +
oth_sp +
s(site, bs="re"),
knots = list(Time=c(0,23)),
family = "binomial",
data = occasions_Co_cbind
)
newdat <- with(occasions_Co_cbind, expand.grid(Time = seq(0, 24, 1),
oth_sp = as.factor(c(0,1)),
site = "10E" #Site doesn't matter
)
)
cycl_pred_Co <- predict.bam(mod_cycl_Co,
newdata = newdat,
exclude = "s(site)",
se.fit = TRUE,
type = "response"
)
cycl_pred_Co <- cbind(newdat,
fit=cycl_pred_Co$fit,
se.fit=cycl_pred_Co$se.fit,
Species = "Coyote"
)
# Wolf
mod_cycl_Wo <- bam(cbind(success, failure) ~ s(Time, bs = "cc", k = 12, by = oth_sp, m = 1) +
oth_sp +
s(site, bs="re"),
knots = list(Time=c(0,23)),
family = "binomial",
data = occasions_Wo_cbind
)
newdat <- with(occasions_Wo_cbind, expand.grid(Time = seq(0, 24, 1),
oth_sp = as.factor(c(0,1)),
site = "10E" #Site doesn't matter
)
)
cycl_pred_Wo <- predict.bam(mod_cycl_Wo,
newdata = newdat,
exclude = "s(site)",
se.fit = TRUE,
type = "response"
)
cycl_pred_Wo <- cbind(newdat,
fit=cycl_pred_Wo$fit,
se.fit=cycl_pred_Wo$se.fit,
Species = "Wolf"
)
cycl_pred <- rbind(cycl_pred_Co, cycl_pred_Wo) %>%
mutate(oth_sp_labels = fct_recode(oth_sp, "Without the other species" = "0", "With the other species" = "1"))pl_cycl <- ggplot(cycl_pred, aes(Time, fit, color=Species, group=Species)) +
geom_ribbon(aes(ymin=fit-1.96*se.fit, ymax=fit+1.96*se.fit, fill=Species), alpha=0.5, size = 0.25) +
geom_line(linewidth = 1) +
labs(x = "Time of Day (Hour)", y = "Predicted Activity Pattern \n (probability)", title = "B: Conditional mean (cyclic cubic spline HGAMs)")+
scale_color_manual(values = c("#E69F00", "#0072B2")) +
scale_fill_manual(values = c("#E69F00", "#0072B2")) +
theme_minimal()+
theme(legend.position = "none",
plot.title = element_text(size=10,face="bold"),
axis.line = element_line(colour = 'black', linetype = 'solid'),
axis.ticks = element_line(colour = 'black', linetype = 'solid'),
axis.title = element_text(size=9,face="bold"),
panel.grid.minor.y = element_blank(),
panel.grid.major.y = element_blank(),
panel.grid.major.x = element_line(colour = 'lightgrey', linetype = 'dashed', linewidth = 0.5),
panel.grid.minor.x = element_blank(),
strip.text = element_text(face = "bold")
) +
scale_x_continuous(breaks=seq(0,24,4), labels=seq(0,24,4)) +
facet_wrap(~oth_sp_labels, scales = "fixed")
pl_trig2 <- pl_trig + labs(title = "A: Marginal mean (trigonometric GLMM)") + theme(legend.position = "none", plot.title = element_text(size=10,face="bold", hjust = 0))
ggarrange(pl_trig2, pl_cycl, nrow = 2, ncol = 1, common.legend = TRUE, legend = "right")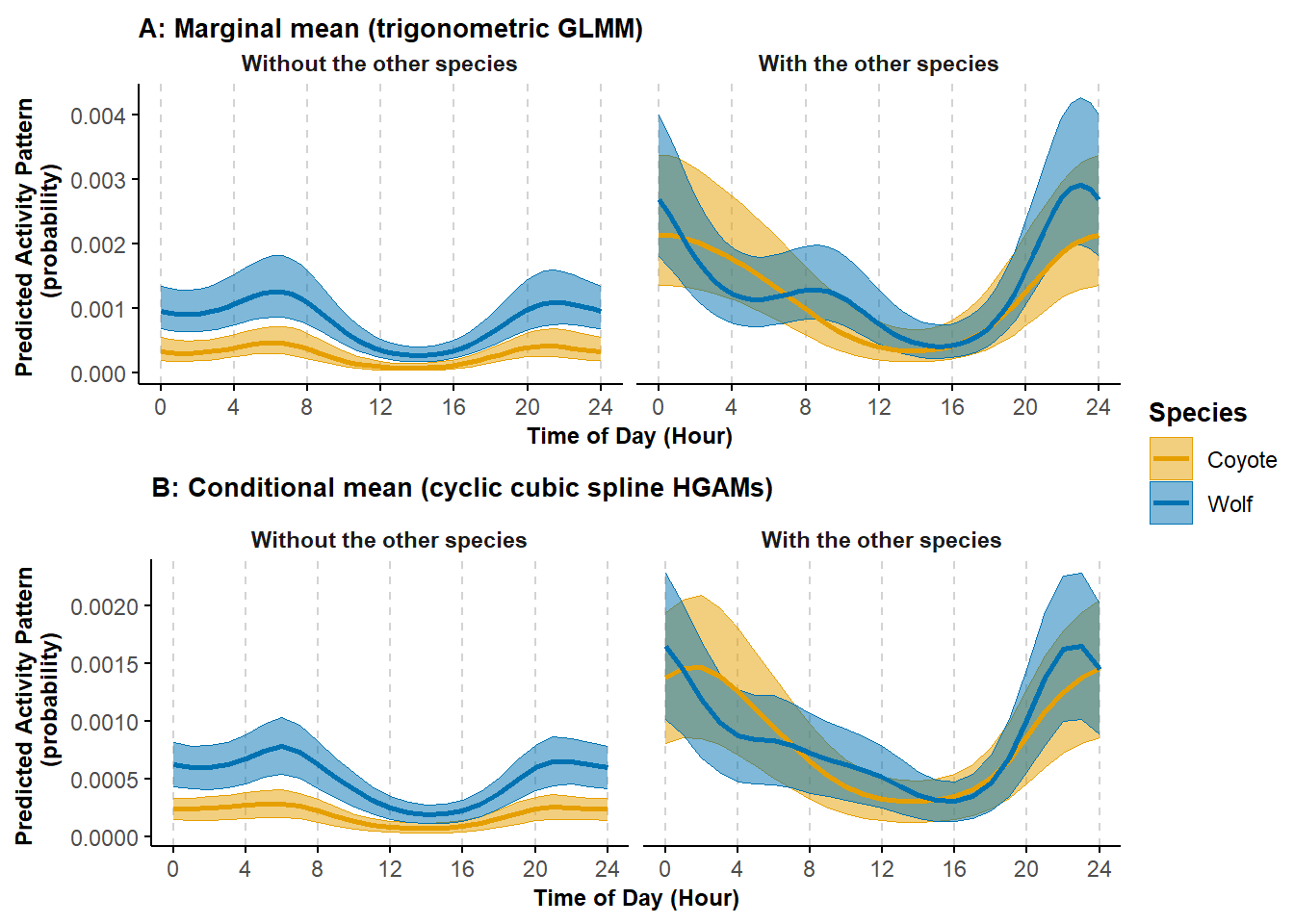
Figure 7.2: Predicted probability of activity by coyote and wolf and depending on each others presence or absence from a trigonometric (A) and cyclic cubic spline (B) hierarhical model; shading corresponds to 95% confidence intervals.
We see that the trigonometric and the cyclic cubic spline hierarchical models return the same general pattern.
Model selection. As with the other examples, we can assess the importance of the presence of the competitor species by comparing models with and without terms involving this covariate (i.e. oth_sp). We fit the reduced model below.
# Trigonometric GLMM (random intercept-only)
# run model: coyote
mod_trig_Co_null <- mixed_model(fixed = cbind(success, failure) ~ cos(2*pi*Time/24) + sin(2*pi*Time/24) +
cos(2*pi*Time/12) + sin(2*pi*Time/12),
random = ~ 1 | site,
family = binomial(),
data = occasions_Co_cbind,
iter_EM = 0
)
# run model: wolf
mod_trig_Wo_null <- mixed_model(fixed = cbind(success, failure) ~ cos(2*pi*Time/24) + sin(2*pi*Time/24) +
cos(2*pi*Time/12) + sin(2*pi*Time/12),
random = ~ 1 | site,
family = binomial(),
data = occasions_Wo_cbind,
iter_EM = 0
) For each of the two species, we can now compare the models that include and do not include the presence of the other species. For coyotes,
## df AIC
## mod_trig_Co_null 6 1576.861
## mod_trig_Co 11 1509.351## [1] 67.5101Based on AIC, there is a strong support for the model that assumes an effect of the presence of wolves as a driver of coyotes’ activity patterns.
## df AIC
## mod_trig_Wo_null 6 2592.905
## mod_trig_Wo 11 2572.546## [1] 20.35866A similar conclusion is reached for the wolf. These results do not imply a casual effect, but rather define an association: in site-sessions where the species co-occur (i.e. in space and time), they tend to have activity patterns that differ compared to site-sessions when they do not co-occur. These differences might be driven by other factors (e.g., level of human disturbance) not considered in the analysis.