Tutorial 3 Estimating activity patterns from time-stamped data

Activity patterns are currently estimated primarily using Kernel Density Estimators (KDEs). However, this approach presents several limitations that we highlight in Iannarilli et al. (2024). In this Tutorial, we introduce two alternative, model-based approaches to estimate activity patterns from time-stamped data:

• trigonometric generalized linear mixed models (trigonometric GLMMs) and

• cyclic cubic spline generalized linear mixed models (cyclic cubic spline HGAMs).

Both types of hierarchical models can accommodate the periodic nature of activity data and also address site-to-site and other forms of variability. Although our examples are all focused on the analysis of camera-trap data, the same framework can be applied to data collected using other static devices (e.g., acoustic recorders) or site-based sampling strategies.

3.1 Simulating activity patterns

To show how trigonometric and cyclic cubic spline hierarchical models can successfully recover the true pattern of activity, we apply these approaches to simulated data. As such, we can compare the estimated patterns to the known, ‘true’, simulated patterns.

To keep the focus on estimating activity patterns, we encapsulate the code to simulate the data in the function sim_activity, that we source after loading the necessary libraries. This function simulates data based on equation 1 (Tutorial 2 and Materials and Results in Iannarilli et al. (2024)). The function is available in the source_functions folder available at https://github.com/FabiolaIannarilli/HMs_Activity; a description of its arguments and outputs is provided in section 10.1.

# Load libraries and function to simulate activity patterns
set.seed(129)
suppressWarnings({ 
  library(dplyr)
  library(GLMMadaptive)
  library(ggpubr)
  library(mgcv)
  library(tidyr)
})
source("source_functions/sim_activity.R")
source("source_functions/sim_to_minute.R")

We simulate site-specific bimodal activity patterns for 100 sites (M) and 30 days (J) using the parameters defined in the code below. We include both variability in frequency of site-use and variability in timing of activity by drawing values of \(\tau_i\) and \(\gamma_i\) from the distributions \(\tau_i \sim N(0,\sigma_\tau)\) and \(\gamma_i \sim N(0,\sigma_\gamma)\), respectively, with \(\sigma_\tau = 1\) and \(\sigma_\gamma = 0.3\).

# Set equations' parameters
M = 100
J = 30
wavelength = 24
n_peak = 2
b0 = -3
b1 = 1 
b2 = 0.7
theta0 = 3
theta1 = 2 
sd_tau = 1
sd_gamma = 0.3
time <- seq(0, 23, length.out = 100)

# simulate data
dat <- sim_activity(M = M, 
                    J = J, 
                    wavelength = wavelength, 
                    n_peak = n_peak, 
                    n_sim = 1, 
                    b0 = b0, 
                    b0_constant = TRUE, # common intercept
                    tau_constant = FALSE, 
                    sdtau = sd_tau, # ~site-specific intercept
                    b1 = b1, 
                    b2 = b2, # amplitude of the cosine terms 
                    theta0 = theta0, 
                    theta1 = theta1, # common phaseshifts for the cosine terms
                    phaseshift_constant = FALSE, 
                    sd_phaseshift = sd_gamma, # site-specific phaseshift (equal for both cosine terms)
                    plot_true_act = FALSE
                    )
#Observe the structure of the new object
str(dat)

## List of 5
##  $ true_activity_prob: num [1:100, 1:720] 0.00354 0.00474 0.00263 0.00297 0.07437 ...
##  $ Conditional       :'data.frame':  513 obs. of  3 variables:
##   ..$ p     : num [1:513] 0.0138 0.0135 0.0133 0.0131 0.0129 ...
##   ..$ time  : num [1:513] 0 0.0469 0.0938 0.1406 0.1875 ...
##   ..$ y_dens: num [1:513] 0.00931 0.00915 0.009 0.00885 0.00871 ...
##  $ Marginal          :'data.frame':  513 obs. of  3 variables:
##   ..$ p     : num [1:513] 0.0233 0.0229 0.0226 0.0222 0.0219 ...
##   ..$ time  : num [1:513] 0 0.0469 0.0938 0.1406 0.1875 ...
##   ..$ y_dens: num [1:513] 0.0115 0.0113 0.0111 0.0109 0.0107 ...
##  $ sim_data          :List of 1
##   ..$ : int [1:100, 1:720] 0 0 0 0 0 1 0 0 0 0 ...
##  $ phaseshift        : num [1:100] 0.4761 -0.3666 -0.0015 -0.2245 -0.1194 ...

The sim_activity function returns a list containing several objects, including the true activity patterns simulated for each of the 100 sites (object: dat$true_activity_prob) and the associated realized patterns (i.e. the encounter data; object: dat$sim_data). The list also contains the values of the conditional and marginal mean probability of activity (objects: dat$Conditional and dat$Marginal, respectively) and site-specific phaseshift values (object: dat$phaseshift).

We access the information for a randomly selected set of these sites and plot their true activity patterns, along with the conditional and marginal mean activity patterns (the red and black curves, respectively, in the following plot).

# Organize data for plotting
sites_i <- sample(x = 1:M, size = 10, replace = FALSE)
sample_sites <- cbind(sites_i, dat$true_activity_prob[sites_i, 0:25]) 
colnames(sample_sites) <- c("sites", 00:24)
sample_sites <- as.data.frame(sample_sites) %>% 
  pivot_longer(cols = -sites, names_to = "time", values_to = "prob")

#plot true conditional and marginal with 10 simulated sites
(pl_sites <- ggplot() +
  geom_line(data = sample_sites, aes(x = as.numeric(time), y = prob, group = sites, color = as.factor(sites)), 
            linewidth = 0.5, alpha = 0.7, linetype = 2) +
  geom_line(data = dat$Conditional, aes(x = time, y = p), linewidth = 1, color = "red", inherit.aes = TRUE) +
  geom_line(data = dat$Marginal, aes(x = time, y = p), linewidth = 1, color = "black", inherit.aes = TRUE) +
  labs(x = "Time of Day", y = "Probability of Activity", title = "C) Variability in frequency of site-use and \n timing of activity", 
       color = "Site_ID")+
  theme_minimal()+
  theme(legend.position = "none",
        legend.title = element_text(size=10,face="bold"),
        legend.text = element_text(size=10,face="bold"),
        axis.line = element_line(colour = 'black', linetype = 'solid'),
        axis.ticks.x = element_line(colour = 'black', linetype = 'solid'),
        axis.title = element_text(size=8,face="bold"),
        axis.text.y = element_blank(),
        plot.title = element_text(size=9,face="bold"),
        panel.grid.minor.y = element_blank(),
        panel.grid.major.y = element_blank(),
        panel.grid.major.x = element_blank(),
        panel.grid.minor.x = element_blank(),
        strip.text = element_text(size = 9, colour = "black", face = "bold", hjust = 0))+
  geom_segment(aes(x=12, y=min(sample_sites$prob), xend=12, yend=min(sample_sites$prob)-0.05), arrow=arrow(length= unit(0.5, "cm")), 
               linewidth = 1, color = "orange", linejoin = "mitre") +
  geom_segment(aes(x=12, y=0.45+0.003, xend=12, yend=0.45+0.053), arrow=arrow(length= unit(0.5, "cm")), 
               linewidth = 1, color = "orange", linejoin = "mitre") +
  geom_segment(aes(x=12 - 0.75, y=max(sample_sites$prob) + 0.02, xend=12 - 7, yend=max(sample_sites$prob) + 0.02), arrow=arrow(length= unit(0.5, "cm")), 
               linewidth = 1, color = "orange", linejoin = "mitre") +
  geom_segment(aes(x=12 + 0.75, y=max(sample_sites$prob) + 0.02, xend=12 + 7, yend=max(sample_sites$prob) + 0.02), arrow=arrow(length= unit(0.5, "cm")), 
               linewidth = 1, color = "orange", linejoin = "mitre") +
  scale_x_continuous(breaks=seq(0,23,length.out=7), labels=seq(0,24,4)))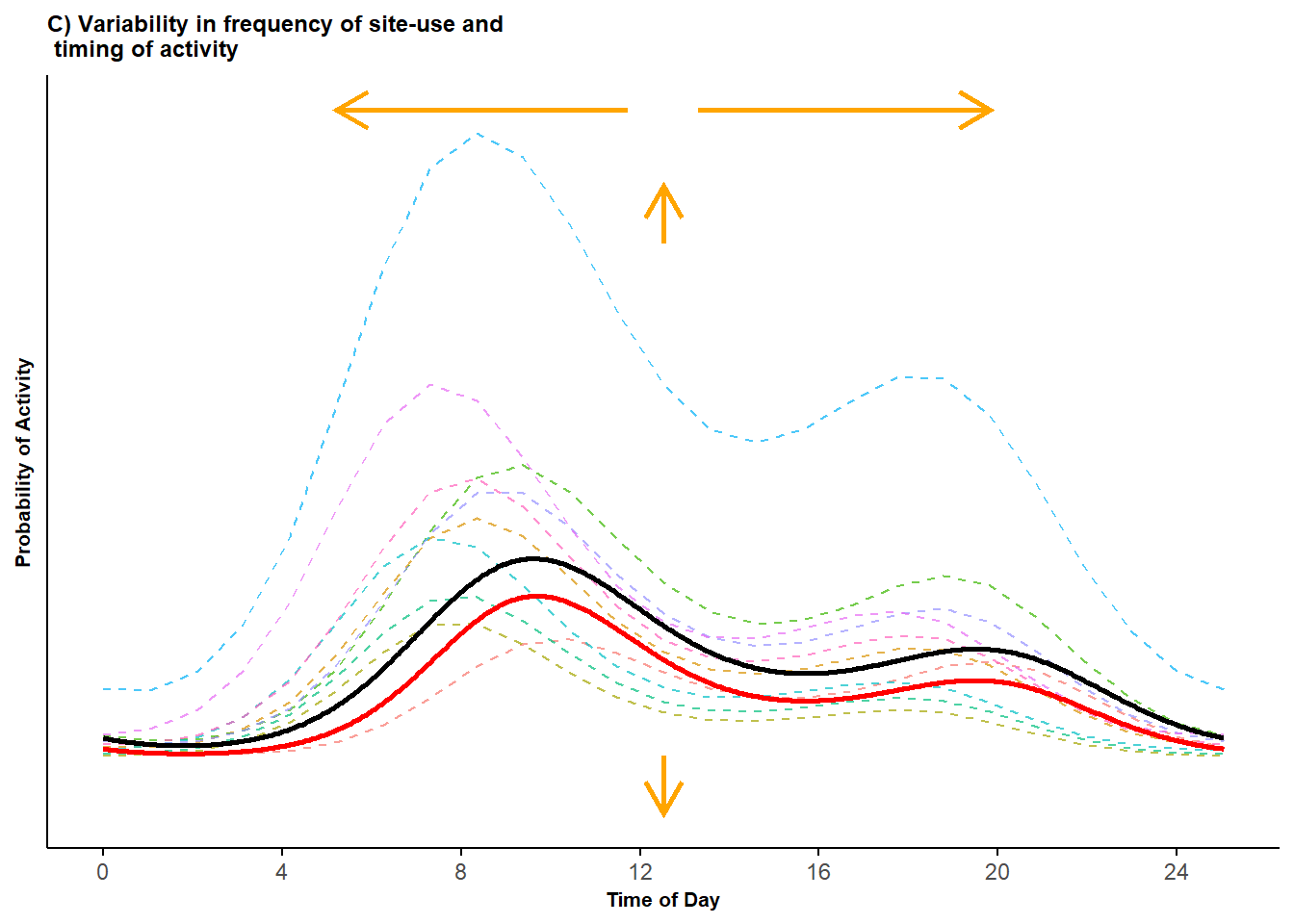

Figure 3.1: Bimodal probability activity curves showing variability in both the frequency of site-use and variability in timing of activity; displayed are activity curves across sites (dashed lines) along with the marginal mean curve (black line) and conditional mean curve (red line).

We see there is considerable variability in the frequency of use among the different sites and relatively smaller variation in timing of activity within the 24-hour cycle.

To create Figure 1 in Iannarilli et al. (2024), we bring together this plot and the two produced in the previous Tutorial.

ggarrange(pl, pl_sites, widths = c(66, 34)) %>%   
ggsave(filename = "ms_figures/Fig1_Site_Variability_in_Activity_bimodal.jpg", 
       device = "jpeg", units = "cm", width = 24, height = 10, dpi = 600
       )

3.2 Data preparation

The first step to analyze the simulated activity patterns is to arrange the simulated encounter data in a specific format. These data are stored in the object sim_data in the list created by the sim_activity function. This object has a number of rows equal to the number of simulated sites (100) and a number of columns equal to 24 (hours) times the length (in days) of the simulated sampling period, which we set to 30 days. This corresponds to 720 columns (\(24 \text{hours} \times 30 \text{days}\)), that is, 720 hourly encounter occasions.

We access the encounter data and store them in an object called y. We add a column that specifies a unique identifier for each site (e.g., id = A1) and assign a name to each of the columns to represent the consecutive time occasions (e.g., from 1 to 720). Then, we reorganize the data from the wide to the long format using the id column as the reference and convert the consecutive time occasions in the relative time of day (e.g., time = 35 is converted to Hour = 11 of the second day of sampling).

# The data
y <- as.data.frame(dat$sim_data)
dim(y)

## [1] 100 720

# summarize aggregated data
y <- data.frame(id=paste("A", seq(1,M,1), sep=""), 
                y=as.data.frame(y)
                )
colnames(y) <- c("id", 
                 paste0("S", seq(1, ncol(y)-1, 1), sep="")
                 )

# Format data in long format
y_long <- pivot_longer(data = y, cols = -id, names_to = "time", values_to = "y") %>%
                mutate(time=as.numeric(substr(time,2,10)),
                       id = factor(id)
                       )

# create variable to describe time as hour (between 0 and 23)
y_long$hour <- sim_to_minute(y_long$time, group = wavelength)

# show first few rows of the dataset created
knitr::kable(head(y_long))

id	time	y	hour
A1	1	0	1
A1	2	0	2
A1	3	0	3
A1	4	0	4
A1	5	0	5
A1	6	0	6

We obtain a dataset in which each row specifies the outcome (i.e. encounter or non-encounter of the target species) at a certain site during a specific hour of a certain day of sampling.

for our analysis, we can use this dataset as it is, considering y as our response variable. Alternatively, we can reduce model fitting computational time by counting the number of hourly-long occasions in which the species was observed (i.e. successes) and the number of occasions in which the species was not observed (i.e. failures) for each combination of hourly time interval (e.g., time = 1) and camera site (e.g. id = A1).

# count successes and failures at each site-occasion
occasions_cbind <- y_long %>% 
  group_by(id, hour) %>% 
  summarise(success = sum(y),
            n_events = n(),
            failure = n_events - success) %>% 
  dplyr::rename(Site = id,
               Time = hour)

## `summarise()` has grouped output by 'id'. You can override using the `.groups` argument.

# show first few rows of the dataset created
knitr::kable(head(occasions_cbind))

Site	Time	success	n_events	failure
A1	0	0	30	30
A1	1	1	30	29
A1	2	0	30	30
A1	3	1	30	29
A1	4	1	30	29
A1	5	0	30	30

In this new version of the dataset, each row specifies how many times a species was (i.e. success: 0 days) and was not (i.e. failure: 30 days) detected at a certain site (Site = A1) during a certain time interval (Time = 0, that is from 00:00 to 00:59). We can now use this dataframe to estimate the diel activity patterns using hierarchical models.

3.3 Trigonometric GLMMs

Equation 1 in Tutorial 2 is non-linear due the presence of the phaseshift parameters. Currently, we are unaware of any out-of-the-box options in the R programming language for fitting trigonometric non-linear mixed models using a frequentist approach. To overcome this challenge, we rewrite equation 1 using compound angle formulas (see also main text Iannarilli et al. (2024)):

\[ \text{logit}(p_t) = \beta_0 + \alpha_1 \times \text{cos}(\frac{2\pi t}{\omega_1}) + \alpha_2 \times \text{sin}(\frac{2\pi t}{\omega_1}) + \alpha_3 \times \text{cos}(\frac{2\pi t}{\omega_2}) + \alpha_4 \times \text{sin}(\frac{2\pi t}{\omega_2}) + \tau_i \] where

\(\alpha_1 = \beta_1 \times \text{cos}(\theta_0 + \gamma_i)\), \(\alpha_2= -\beta_1 \times \text{sin}(\theta_0 + \gamma_i)\), \(\alpha_3= \beta_2 \times \text{cos}(\theta_1 + \gamma_i)\), and \(\alpha_4= -\beta_2 \times \text{sin}(\theta_1 + \gamma_i)\).

In this version (labeled as equation 2 in Iannarilli et al. (2024)), we can model activity patterns using any R package available for fitting GLMMs; we list some of these options in Tables 1 and 2 in Iannarilli et al. (2024). Here, we choose the GLMMadaptive library (Rizopoulos 2022) because it facilitates estimation of both conditional and marginal mean activity patterns (see Tutorial 8).

The simplest trigonometric GLMM we can run is one that includes only a random intercept. In the context of estimating activity patterns, a random intercept-only model accounts for variability in the frequency of site-use (i.e. vertical shifts among the curves), but not variability in the timing of activity (i.e. horizontal shift).

# run model
trig_rand_int <- mixed_model(fixed = cbind(success, failure) ~ 
                              cos(2 * pi * Time/24)  + sin(2 * pi * Time/24) +
                              cos(2 * pi * Time/12)  + sin(2 * pi * Time/12),
                             random = ~  1  |   Site, 
                             data = occasions_cbind, 
                             family = binomial(), 
                             iter_EM = 0
                             )
summary(trig_rand_int)

## 
## Call:
## mixed_model(fixed = cbind(success, failure) ~ cos(2 * pi * Time/24) + 
##     sin(2 * pi * Time/24) + cos(2 * pi * Time/12) + sin(2 * pi * 
##     Time/12), random = ~1 | Site, data = occasions_cbind, family = binomial(), 
##     iter_EM = 0)
## 
## Data Descriptives:
## Number of Observations: 2400
## Number of Groups: 100 
## 
## Model:
##  family: binomial
##  link: logit 
## 
## Fit statistics:
##    log.Lik      AIC      BIC
##  -3742.866 7497.732 7513.363
## 
## Random effects covariance matrix:
##                StdDev
## (Intercept) 0.9725664
## 
## Fixed effects:
##                       Estimate Std.Err  z-value p-value
## (Intercept)            -3.0670  0.0998 -30.7257 < 1e-04
## cos(2 * pi * Time/24)  -0.9339  0.0263 -35.5111 < 1e-04
## sin(2 * pi * Time/24)  -0.1321  0.0220  -6.0164 < 1e-04
## cos(2 * pi * Time/12)  -0.2802  0.0225 -12.4511 < 1e-04
## sin(2 * pi * Time/12)  -0.5891  0.0229 -25.7027 < 1e-04
## 
## Integration:
## method: adaptive Gauss-Hermite quadrature rule
## quadrature points: 11
## 
## Optimization:
## method: quasi-Newton
## converged: TRUE

For trigonometric models, it is difficult to interpret the coefficients. An easier and effective way to explore these results is to visually check the activity patterns predicted based on the model itself. Thus, we predict the estimated (conditional) activity pattern, backtrasform the results from logit to the probability scale, and plot the estimated activity pattern along with the true simulated (conditional mean) activity pattern.

# estimated activity pattern
newdat <- with(occasions_cbind, expand.grid(Time = seq(min(Time), 24, length.out = 48)))
cond_eff0 <- effectPlotData(trig_rand_int, newdat, marginal = FALSE) %>% 
  mutate(pred = plogis(pred),
         low = plogis(low),
         upp = plogis(upp),
         Mod = "Estimated: Random Intercept-only")

# simulated conditional activity pattern
cond_true <- dat$Conditional %>% 
  mutate(low = NA,
         upp = NA,
         Mod = "Simulated Conditional") %>% 
  dplyr::rename(Time = time, pred = p) %>% 
  select(Time, pred, low, upp, Mod)

# combine the two for visualization  purposes
cond_eff <- rbind(cond_true, cond_eff0)

# plot
(pl_trig1 <- ggplot(cond_eff, aes(Time, pred)) +
  geom_ribbon(aes(ymin = low, ymax = upp, color = Mod, fill = Mod), alpha = 0.3, linewidth = 0.25) + 
  geom_line(aes(color = Mod), linewidth = 1) + #
  scale_color_manual(values = c("blue", "red")) +
  scale_fill_manual(values = c("blue", "red")) +
  labs(x = "Time of Day (Hour)", y = "Predicted Activity Pattern \n (probability)", title = "Estimated vs Simulated Activity Patterns")+
  theme_minimal()+
  theme(legend.position = "bottom",
        legend.title = element_blank(),
        legend.text = element_text(size=10,face="bold"),
        legend.margin=margin(0,0,0,0),
        legend.box.margin=margin(-5,-10,-10,-10),
        plot.title = element_text(size=10,face="bold"),
        axis.line = element_line(colour = 'black', linetype = 'solid'),
        axis.ticks = element_line(colour = 'black', linetype = 'solid'),
        axis.title = element_text(size=9,face="bold"),
        panel.grid.minor.y = element_blank(),
        panel.grid.major.y = element_blank(),
        panel.grid.major.x = element_line(colour = 'lightgrey', linetype = 'dashed', linewidth=0.5),
        panel.grid.minor.x = element_blank(),
        strip.text = element_text(size = 9, colour = "black", face = "bold", hjust = 0),
        plot.margin = margin(0.1,0.1,0.5,0.1, "cm"))+
  scale_x_continuous(breaks=seq(0,23,length.out=7), labels=seq(0,24,4)))

## Warning in max(ids, na.rm = TRUE): no non-missing arguments to max; returning -Inf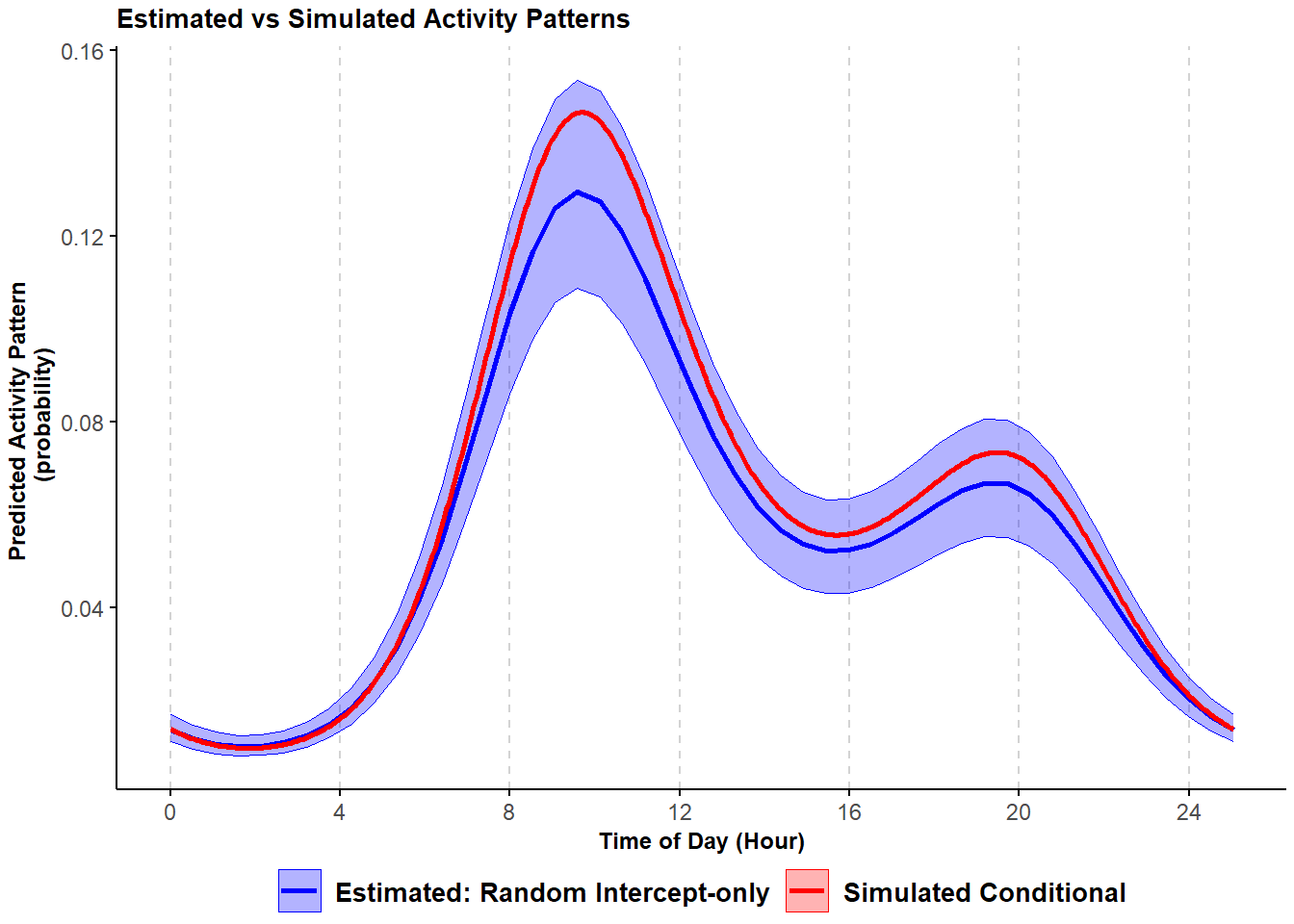

Figure 3.2: Comparison of simulated and estimated probability of activity conditional mean curves with variability in the frequency of site-use from a trigonometric hierarchical model; shading corresponds to 95% confidence intervals.

The estimated activity pattern from the random intercept-only trigonometric GLMM (in blue) closely resembles the simulated conditional probability (in red) even though we ignored site-to-site variability in the timing of activity.

To allow site-to-site variability in the timing of activity, we can add random slopes to the model. The choice of the structure of the random slope effect is not trivial; we can include only parameters linked to the first cosine term in equation 1 (i.e. first two terms in equation 2), only terms for the second cosine term in equation 2 (i.e. third and forth terms in equation 2) or both. When possible, based on computational time and the information contained in the data, we recommend to include all the terms and allow for the random intercept to vary independently of the random slope¹. In GLMMadaptive, we ensure this independence by using the syntax || when specifying the random effect component of the model. In Table 2 in Iannarilli et al. (2024), we provide guidance on the code syntax needed to run the equivalent model and the other models presented throughout the tutorial with other R packages.

# run model
trig_rand_slope <- mixed_model(fixed = cbind(success, failure) ~ 
                                  cos(2 * pi * Time/24)  + sin(2 * pi * Time/24) +
                                  cos(2 * pi * Time/12)  + sin(2 * pi * Time/12),
                               random = ~  cos(2 * pi * Time/24)  + sin(2 * pi * Time/24) +
                                        cos(2 * pi * Time/12)  + sin(2 * pi * Time/12)  ||   Site,
                               data = occasions_cbind, 
                               family = binomial(), 
                               iter_EM = 0
                               )

summary(trig_rand_slope)

## 
## Call:
## mixed_model(fixed = cbind(success, failure) ~ cos(2 * pi * Time/24) + 
##     sin(2 * pi * Time/24) + cos(2 * pi * Time/12) + sin(2 * pi * 
##     Time/12), random = ~cos(2 * pi * Time/24) + sin(2 * pi * 
##     Time/24) + cos(2 * pi * Time/12) + sin(2 * pi * Time/12) || 
##     Site, data = occasions_cbind, family = binomial(), iter_EM = 0)
## 
## Data Descriptives:
## Number of Observations: 2400
## Number of Groups: 100 
## 
## Model:
##  family: binomial
##  link: logit 
## 
## Fit statistics:
##    log.Lik      AIC      BIC
##  -3704.187 7428.374 7454.425
## 
## Random effects covariance matrix:
##                       StdDev
## (Intercept)           0.9742
## cos(2 * pi * Time/24) 0.0307
## sin(2 * pi * Time/24) 0.2343
## cos(2 * pi * Time/12) 0.1913
## sin(2 * pi * Time/12) 0.0430
## 
## Fixed effects:
##                       Estimate Std.Err  z-value p-value
## (Intercept)            -3.0888  0.1000 -30.8945 < 1e-04
## cos(2 * pi * Time/24)  -0.9410  0.0268 -35.1529 < 1e-04
## sin(2 * pi * Time/24)  -0.1584  0.0345  -4.5927 < 1e-04
## cos(2 * pi * Time/12)  -0.2659  0.0315  -8.4323 < 1e-04
## sin(2 * pi * Time/12)  -0.5988  0.0237 -25.2223 < 1e-04
## 
## Integration:
## method: adaptive Gauss-Hermite quadrature rule
## quadrature points: 7
## 
## Optimization:
## method: quasi-Newton
## converged: TRUE

As before, we visually inspect the estimated conditional mean activity pattern based on this model and compare it with the simulated conditional mean activity pattern.

# estimated activity pattern
newdat <- with(occasions_cbind, expand.grid(Time = seq(min(Time), 24, length.out = 48)))
cond_eff1 <- effectPlotData(trig_rand_slope, newdat, marginal = FALSE) %>% 
  mutate(pred = plogis(pred),
         low = plogis(low),
         upp = plogis(upp),
         Mod = "Estimated: Random Intercept and Slope")

# simulated conditional activity pattern
cond_true <- dat$Conditional %>% 
  mutate(low = NA,
         upp = NA,
         Mod = "Simulated Conditional") %>% 
  dplyr::rename(Time = time, pred = p) %>% 
  select(Time, pred, low, upp, Mod)

# combine the two for visualization  purposes
cond_eff <- rbind(cond_true, cond_eff1)

# plot
(pl_trig2 <- ggplot(cond_eff, aes(Time, pred)) +
  geom_ribbon(aes(ymin = low, ymax = upp, color = Mod, fill = Mod), alpha = 0.3, linewidth = 0.25) + #
  geom_line(aes(color = Mod), linewidth = 1) + #
  scale_color_manual(values = c("blue", "red")) +
  scale_fill_manual(values = c("blue", "red")) +
  labs(x = "Time of Day (Hour)", y = "Predicted Activity Pattern \n (probability)", 
       title = "Estimated vs Simulated Activity Patterns"
       )+
  theme_minimal()+
  theme(legend.position = "bottom",
        legend.title = element_blank(),
        legend.text = element_text(size=10,face="bold"),
        legend.margin=margin(0,0,0,0),
        legend.box.margin=margin(-5,-10,-10,-10),
        plot.title = element_text(size=10,face="bold"),
        axis.line = element_line(colour = 'black', linetype = 'solid'),
        axis.ticks = element_line(colour = 'black', linetype = 'solid'),
        axis.title = element_text(size=9,face="bold"),
        panel.grid.minor.y = element_blank(),
        panel.grid.major.y = element_blank(),
        panel.grid.major.x = element_line(colour = 'lightgrey', linetype = 'dashed', linewidth=0.5),
        panel.grid.minor.x = element_blank(),
        strip.text = element_text(size = 9, colour = "black", face = "bold", hjust = 0),
        plot.margin = margin(0.1,0.1,0.5,0.1, "cm")
        )+
  scale_x_continuous(breaks=seq(0,23,length.out=7), labels=seq(0,24,4))
)

## Warning in max(ids, na.rm = TRUE): no non-missing arguments to max; returning -Inf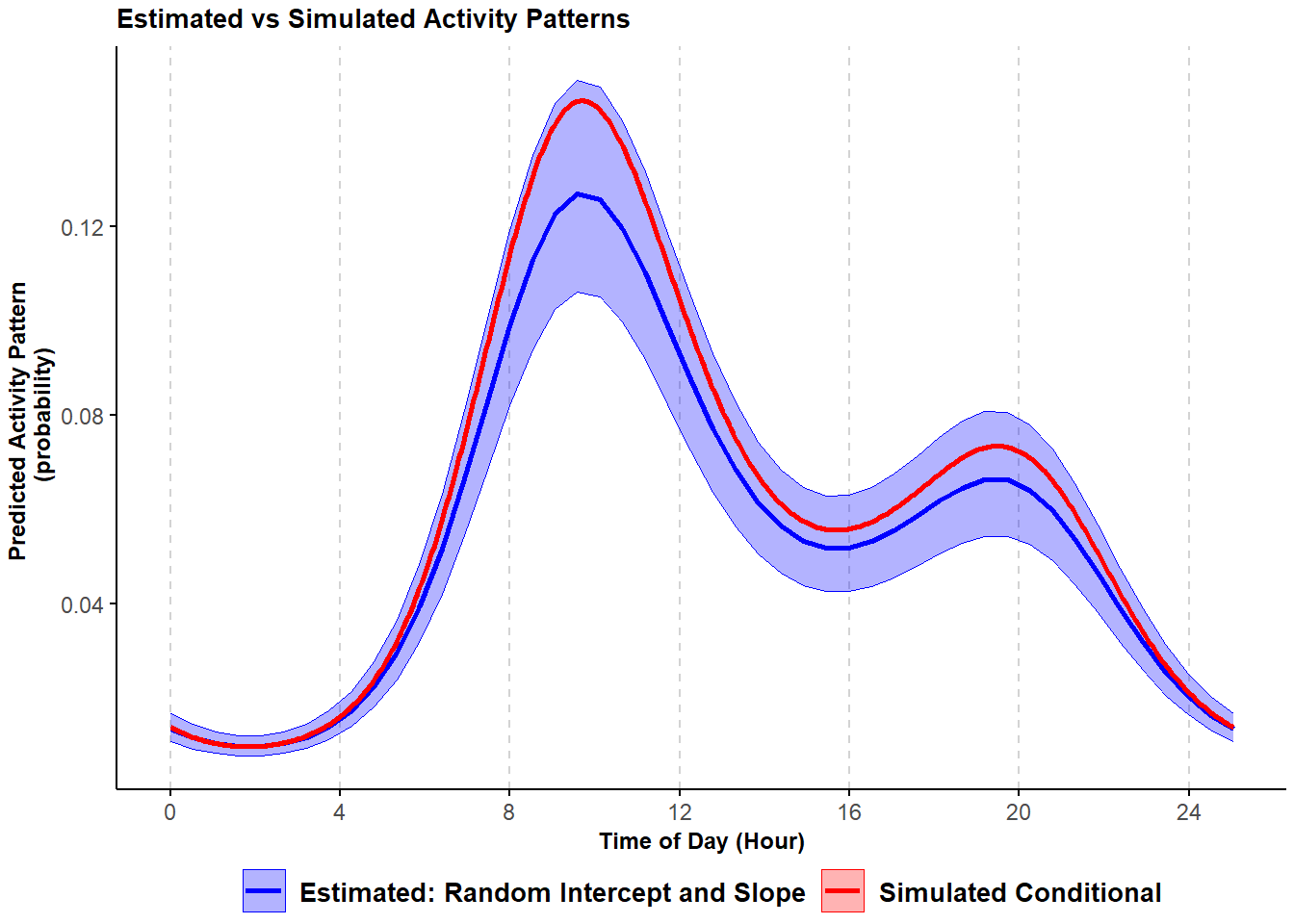

Figure 3.3: Comparison of simulated and estimated probability of activity conditional mean curve with variability in the frequency of site-use and timing of activity from a trigonometric hierarchical model; shading corresponds to 95% confidence intervals.

Again, the estimated activity curve closely matches the true activity that was used to generate the data. In this case, adding a random slope improved the estimates only marginally. This will often be the case when there is only a low level of variation in the timing of activity across sites (Iannarilli 2020), as occurs in the data we simulated. In section 6.1, we consider an example in which modelling variability in the timing of activity reveals interesting site-to-site differences in activity patterns.

3.4 Cyclic cubic spline HGAMs

In this section, we illustrate how cyclic cubic spline HGAMs can be used to explore activity patterns. HGAMs, of which cyclic cubic spline hierarchical models are a special case, are complex functions that allow analysts to model non-linear relationships. These models are highly flexible, often computationally intensive for large datasets, and can be used to model a wide array of model structures and related hypotheses. This high flexibility can make these models intimidating at first. A complete review of the different proprieties of these models is beyond the scope of this work (but see Pedersen et al. (2019) and S. N. Wood (2017b)). Here, we present two model structures that, in our opinion, are useful when addressing the most common ecological questions related to activity patterns.

We fit a cyclic cubic spline hierarchical model using the bam function in package mgcv (S. N. Wood 2017b). We start with a model that resembles a trigonometric random intercept-only model. We use the argument bs="re" in the smoother s(Site, bs="re") to specify Site as a random intercept. We also have a cyclic cubic smoother for Time that accommodates the periodicity in the data. As before, we run the model, predict the estimated activity pattern using the predict.bam function available in the mgcv package (S. N. Wood 2017b), and visually compare it with the simulated conditional mean activity pattern.

# run model
cycl_rand_int <- bam(cbind(success, failure) ~ s(Time, bs = "cc", k = 12) + 
                                               s(Site, bs="re"), 
                                               family = "binomial", 
                                               data = occasions_cbind, 
                                               knots = list(Time=c(0,23))
                     ) 
summary(cycl_rand_int)

## 
## Family: binomial 
## Link function: logit 
## 
## Formula:
## cbind(success, failure) ~ s(Time, bs = "cc", k = 12) + s(Site, 
##     bs = "re")
## 
## Parametric coefficients:
##             Estimate Std. Error z value Pr(>|z|)    
## (Intercept) -3.04745    0.09894   -30.8   <2e-16 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Approximate significance of smooth terms:
##            edf Ref.df Chi.sq p-value    
## s(Time)  9.066     10   3094  <2e-16 ***
## s(Site) 95.262     99   3687  <2e-16 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## R-sq.(adj) =   0.76   Deviance explained = 70.6%
## fREML =   3722  Scale est. = 1         n = 2400

# build estimated activity curves
newdat <- with(occasions_cbind, 
               expand.grid(Time = seq(min(Time), max(Time), 1),
                           Site = "A1") #Site doesn't matter
               ) 
temp <- predict.bam(cycl_rand_int, newdata = newdat,  exclude = "s(Site)", se.fit = TRUE, type = "response") 
cycl_pred <- newdat  %>% 
  mutate(pred = temp$fit,
         low = pred - 1.96*temp$se.fit,
         upp = pred + 1.96*temp$se.fit,
         Mod = "Estimated: Random Intercept-only") %>% 
  select(-Site)

# combine true and estimated curves for visualization  purposes
cond_eff <- rbind(cond_true, cycl_pred)

# plot
(pl_cycl1 <- ggplot(cond_eff, aes(Time, pred)) +
  geom_ribbon(aes(ymin = low, ymax = upp, color = Mod, fill = Mod), alpha = 0.3, linewidth = 0.25) + 
  geom_line(aes(color = Mod), linewidth = 1) + 
  scale_color_manual(values = c("blue", "red")) +
  scale_fill_manual(values = c("blue", "red")) +
  labs(x = "Time of Day (Hour)", y = "Predicted Activity Pattern \n (probability)", 
       title = "Estimated vs Simulated Activity Patterns"
       )+
  theme_minimal()+
  theme(legend.position = "bottom",
        legend.title = element_blank(),
        legend.text = element_text(size=10,face="bold"),
        legend.margin=margin(0,0,0,0),
        legend.box.margin=margin(-5,-10,-10,-10),
        plot.title = element_text(size=10,face="bold"),
        axis.line = element_line(colour = 'black', linetype = 'solid'),
        axis.ticks = element_line(colour = 'black', linetype = 'solid'),
        axis.title = element_text(size=9,face="bold"),
        panel.grid.minor.y = element_blank(),
        panel.grid.major.y = element_blank(),
        panel.grid.major.x = element_line(colour = 'lightgrey', linetype = 'dashed', linewidth=0.5),
        panel.grid.minor.x = element_blank(),
        strip.text = element_text(size = 9, colour = "black", face = "bold", hjust = 0),
        plot.margin = margin(0.1,0.1,0.5,0.1, "cm")
        )+
  scale_x_continuous(breaks=seq(0,23,length.out=7), labels=seq(0,24,4))
)

## Warning in max(ids, na.rm = TRUE): no non-missing arguments to max; returning -Inf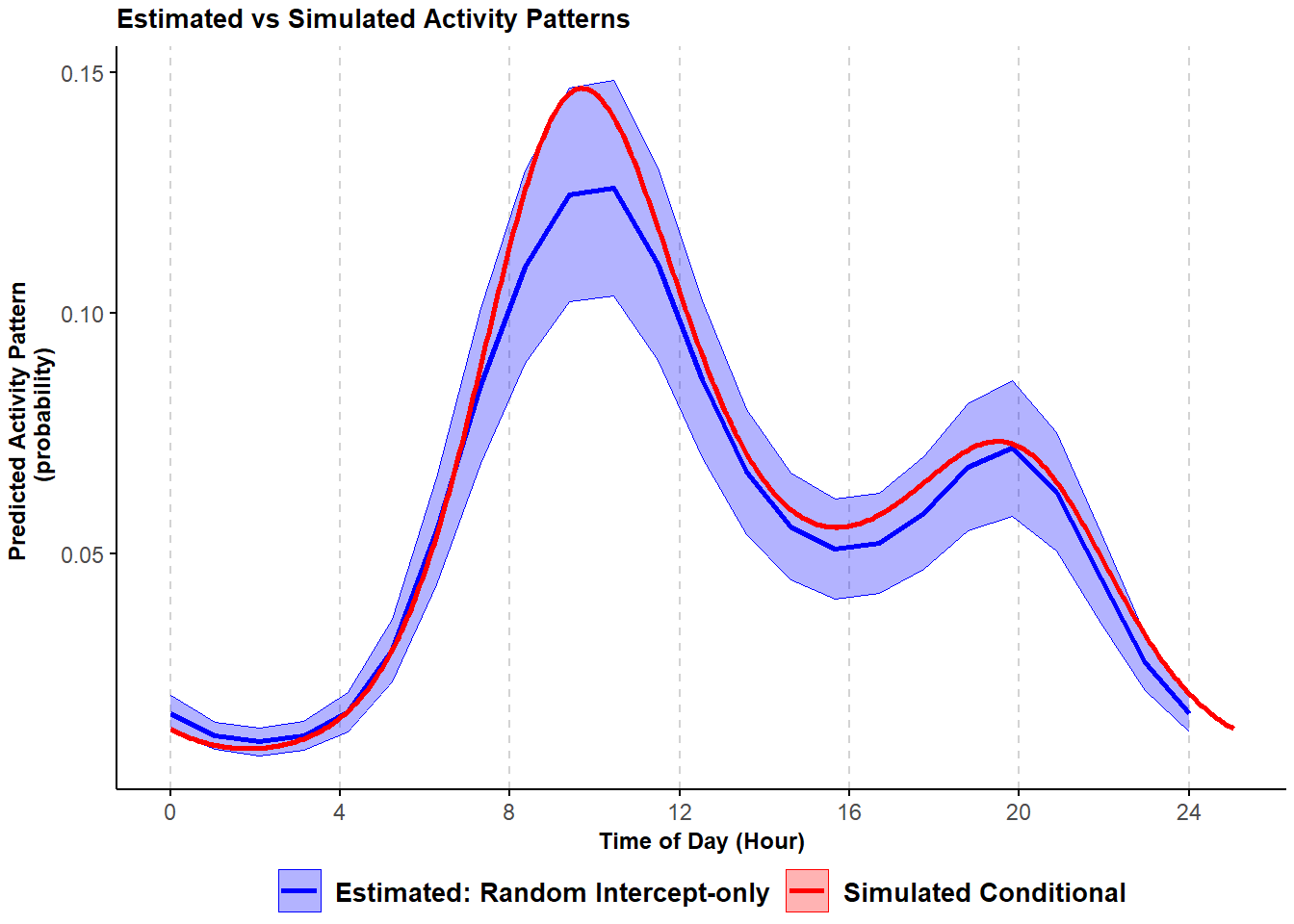

Figure 3.4: Comparison of simulated and HGAM estimated probability of activity conditional mean curves with variability in the frequency of site-use; shading corresponds to 95% confidence intervals.

This model corresponds, in general terms, to the trigonometric random intercept-only model we ran earlier. Thus, it only accommodates variability in the frequency of site-use and not in the timing of activity. The model again captures the general shape of the simulated conditional mean activity curve.

We can add complexity and include a smoother that shrinks the site-specific estimates toward a common smooth and one that allows curves to vary among sites. This model structure resembles the random slope component in trigonometric random intercept and random slope models and allows the site-specific estimates to vary also in the timing of activity. In mgcv, there is no need to explicitly force the independence between the random intercept and the random slope (as done before for the trigonometric hierarchical models) because there is no covariance term between two random effects.

# Fit model with general smoother for Time
cycl_rand_slope <- bam(cbind(success, failure) ~ 
                       s(Time, bs = "cc", k = 12) + # general smoother
                       s(Time, bs = "cc", k = 12, by = Site, m = 1) +
                       s(Site, bs="re"), 
                       knots = list(Time=c(0,23)),
                       family = "binomial", 
                       data = occasions_cbind
                       )
summary(cycl_rand_slope)

## 
## Family: binomial 
## Link function: logit 
## 
## Formula:
## cbind(success, failure) ~ s(Time, bs = "cc", k = 12) + s(Time, 
##     bs = "cc", k = 12, by = Site, m = 1) + s(Site, bs = "re")
## 
## Parametric coefficients:
##             Estimate Std. Error z value Pr(>|z|)    
## (Intercept) -3.05918    0.09874  -30.98   <2e-16 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Approximate significance of smooth terms:
##                        edf Ref.df   Chi.sq p-value    
## s(Time)          9.061e+00     10 2583.131  <2e-16 ***
## s(Time):SiteA1   4.371e-01     10    0.562  0.3830    
## s(Time):SiteA10  2.003e-06     10    0.000  0.7101    
## s(Time):SiteA100 1.420e+00     10    3.306  0.4797    
## s(Time):SiteA11  1.797e-06     10    0.000  0.5936    
## s(Time):SiteA12  1.832e-06     10    0.000  0.7132    
## s(Time):SiteA13  1.639e+00     10    9.885  0.2819    
## s(Time):SiteA14  1.527e-06     10    0.000  0.5203    
## s(Time):SiteA15  2.331e+00     10   42.828  0.0452 *  
## s(Time):SiteA16  2.205e-06     10    0.000  0.5133    
## s(Time):SiteA17  8.433e-01     10    3.353  0.1922    
## s(Time):SiteA18  2.039e-06     10    0.000  0.7737    
## s(Time):SiteA19  3.553e+00     10   62.047  0.0412 *  
## s(Time):SiteA2   3.703e-06     10    0.000  0.5109    
## s(Time):SiteA20  3.998e+00     10   31.694  0.2002    
## s(Time):SiteA21  4.114e+00     10   46.728  0.0393 *  
## s(Time):SiteA22  1.198e-06     10    0.000  0.7510    
## s(Time):SiteA23  7.953e-06     10    0.000  0.4636    
## s(Time):SiteA24  9.795e-01     10    1.770  0.4597    
## s(Time):SiteA25  3.840e-06     10    0.000  0.4801    
## s(Time):SiteA26  2.197e+00     10  111.557  0.0144 *  
## s(Time):SiteA27  9.035e-07     10    0.000  0.9599    
## s(Time):SiteA28  2.784e-06     10    0.000  0.5393    
## s(Time):SiteA29  3.745e+00     10   33.511  0.1217    
## s(Time):SiteA3   5.584e-06     10    0.000  0.3965    
## s(Time):SiteA30  9.305e-07     10    0.000  0.9744    
## s(Time):SiteA31  2.444e-06     10    0.000  0.5635    
## s(Time):SiteA32  4.038e-02     10    0.045  0.3373    
## s(Time):SiteA33  2.085e-06     10    0.000  0.7380    
## s(Time):SiteA34  2.818e-06     10    0.000  0.5247    
## s(Time):SiteA35  1.054e-06     10    0.000  0.9977    
## s(Time):SiteA36  2.531e-01     10    0.357  0.3264    
## s(Time):SiteA37  4.911e-06     10    0.000  0.4435    
## s(Time):SiteA38  1.429e+00     10    5.344  0.3602    
## s(Time):SiteA39  1.353e-06     10    0.000  0.8886    
## s(Time):SiteA4   1.213e-06     10    0.000  0.8443    
## s(Time):SiteA40  3.242e-01     10    0.513  0.2930    
## s(Time):SiteA41  2.556e-01     10    0.415  0.2784    
## s(Time):SiteA42  1.115e+00     10    2.887  0.3039    
## s(Time):SiteA43  2.661e-06     10    0.000  0.5941    
## s(Time):SiteA44  1.061e-06     10    0.000  0.5674    
## s(Time):SiteA45  9.063e-03     10    0.009  0.3550    
## s(Time):SiteA46  9.732e-01     10    4.958  0.1412    
## s(Time):SiteA47  2.472e-02     10    0.027  0.3410    
## s(Time):SiteA48  1.970e-06     10    0.000  0.6506    
## s(Time):SiteA49  1.070e-06     10    0.000  0.9658    
## s(Time):SiteA5   8.967e-07     10    0.000  0.7955    
## s(Time):SiteA50  1.559e+00     10    5.293  0.0700 .  
## s(Time):SiteA51  3.052e-06     10    0.000  0.5682    
## s(Time):SiteA52  7.708e-07     10    0.000  0.8218    
## s(Time):SiteA53  1.784e+00     10   19.804  0.1444    
## s(Time):SiteA54  8.030e-06     10    0.000  0.4270    
## s(Time):SiteA55  1.913e-06     10    0.000  0.5856    
## s(Time):SiteA56  9.627e-01     10   12.752  0.0569 .  
## s(Time):SiteA57  9.381e-01     10    6.027  0.1786    
## s(Time):SiteA58  1.025e-06     10    0.000  0.9562    
## s(Time):SiteA59  7.248e-01     10    1.168  0.5292    
## s(Time):SiteA6   4.144e+00     10   49.389  0.1140    
## s(Time):SiteA60  1.565e-06     10    0.000  0.8538    
## s(Time):SiteA61  1.103e-06     10    0.000  0.9148    
## s(Time):SiteA62  2.243e-06     10    0.000  0.5242    
## s(Time):SiteA63  1.178e-05     10    0.000  0.4258    
## s(Time):SiteA64  2.117e+00     10   62.976  0.0260 *  
## s(Time):SiteA65  2.724e+00     10   37.437  0.0981 .  
## s(Time):SiteA66  1.809e+00     10   15.902  0.1948    
## s(Time):SiteA67  1.534e-06     10    0.000  0.7535    
## s(Time):SiteA68  2.834e-06     10    0.000  0.5173    
## s(Time):SiteA69  2.151e-01     10    0.257  0.3358    
## s(Time):SiteA7   4.642e-06     10    0.000  0.4472    
## s(Time):SiteA70  4.617e-01     10    2.428  0.1073    
## s(Time):SiteA71  1.383e-06     10    0.000  0.5298    
## s(Time):SiteA72  9.419e-01     10    2.310  0.2210    
## s(Time):SiteA73  4.981e-06     10    0.000  0.5110    
## s(Time):SiteA74  6.739e-02     10    0.072  0.3742    
## s(Time):SiteA75  1.080e-01     10    0.156  0.3083    
## s(Time):SiteA76  5.645e-01     10    0.855  0.4055    
## s(Time):SiteA77  9.215e-07     10    0.000  0.6584    
## s(Time):SiteA78  1.210e+00     10    3.184  0.3880    
## s(Time):SiteA79  1.114e+00     10    4.934  0.2169    
## s(Time):SiteA8   7.637e-07     10    0.000  0.6840    
## s(Time):SiteA80  2.614e+00     10   11.273  0.3388    
## s(Time):SiteA81  2.436e-03     10    0.002  0.3616    
## s(Time):SiteA82  7.592e-01     10    1.556  0.3970    
## s(Time):SiteA83  1.134e+00     10   13.496  0.0943 .  
## s(Time):SiteA84  9.353e-06     10    0.000  0.4141    
## s(Time):SiteA85  2.802e-06     10    0.000  0.4922    
## s(Time):SiteA86  2.003e+00     10   11.026  0.2890    
## s(Time):SiteA87  2.833e-06     10    0.000  0.6427    
## s(Time):SiteA88  2.636e-06     10    0.000  0.8619    
## s(Time):SiteA89  1.315e+00     10    5.537  0.2723    
## s(Time):SiteA9   1.040e+00     10    2.502  0.4632    
## s(Time):SiteA90  1.151e+00     10   20.161  0.0376 *  
## s(Time):SiteA91  1.381e-06     10    0.000  0.8268    
## s(Time):SiteA92  1.346e-06     10    0.000  0.9748    
## s(Time):SiteA93  9.053e-07     10    0.000  0.8641    
## s(Time):SiteA94  3.807e-02     10    0.039  0.3685    
## s(Time):SiteA95  6.342e-01     10    2.482  0.1206    
## s(Time):SiteA96  3.957e-06     10    0.000  0.5196    
## s(Time):SiteA97  5.507e-06     10    0.000  0.4437    
## s(Time):SiteA98  1.013e-06     10    0.000  0.7219    
## s(Time):SiteA99  2.401e+00     10   23.757  0.0874 .  
## s(Site)          9.506e+01     99 3527.045  <2e-16 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## R-sq.(adj) =  0.794   Deviance explained = 73.8%
## fREML = 3656.1  Scale est. = 1         n = 2400

# build the estimated activity patterns
newdat <- with(occasions_cbind, 
               expand.grid(Time = seq(min(Time), max(Time), 1), 
                           Site = "A1" #Site doesn't matter
                           )  
               )
temp <- predict.bam(cycl_rand_slope, 
                    newdata = newdat,  
                    exclude = "s(Site)", 
                    se.fit = TRUE, 
                    type = "response"
                    )

cycl_pred <- newdat  %>% 
  mutate(pred = temp$fit,
         low = pred - 1.96*temp$se.fit,
         upp = pred + 1.96*temp$se.fit,
         Mod = "Estimated: Random Slope") %>% 
  select(-Site)

# combine the true and estimated curves for visualization  purposes
cond_eff <- rbind(cond_true, cycl_pred)

# plot
(pl_cycl2 <- ggplot(cond_eff, aes(Time, pred)) +
  geom_ribbon(aes(ymin = low, ymax = upp, color = Mod, fill = Mod), alpha = 0.3, linewidth = 0.25) + #
  geom_line(aes(color = Mod), linewidth = 1) + #
  scale_color_manual(values = c("blue", "red")) +
  scale_fill_manual(values = c("blue", "red")) +
  labs(x = "Time of Day (Hour)", y = "Predicted Activity Pattern \n (probability)", 
       title = "Estimated vs Simulated Activity Patterns"
       )+
  theme_minimal()+
  theme(legend.position = "bottom",
        legend.title = element_blank(),
        legend.text = element_text(size=10,face="bold"),
        legend.margin=margin(0,0,0,0),
        legend.box.margin=margin(-5,-10,-10,-10),
        plot.title = element_text(size=10,face="bold"),
        axis.line = element_line(colour = 'black', linetype = 'solid'),
        axis.ticks = element_line(colour = 'black', linetype = 'solid'),
        axis.title = element_text(size=9,face="bold"),
        panel.grid.minor.y = element_blank(),
        panel.grid.major.y = element_blank(),
        panel.grid.major.x = element_line(colour = 'lightgrey', linetype = 'dashed', linewidth=0.5),
        panel.grid.minor.x = element_blank(),
        strip.text = element_text(size = 9, colour = "black", face = "bold", hjust = 0),
        plot.margin = margin(0.1,0.1,0.5,0.1, "cm"))+
  scale_x_continuous(breaks=seq(0,23,length.out=7), labels=seq(0,24,4)))

## Warning in max(ids, na.rm = TRUE): no non-missing arguments to max; returning -Inf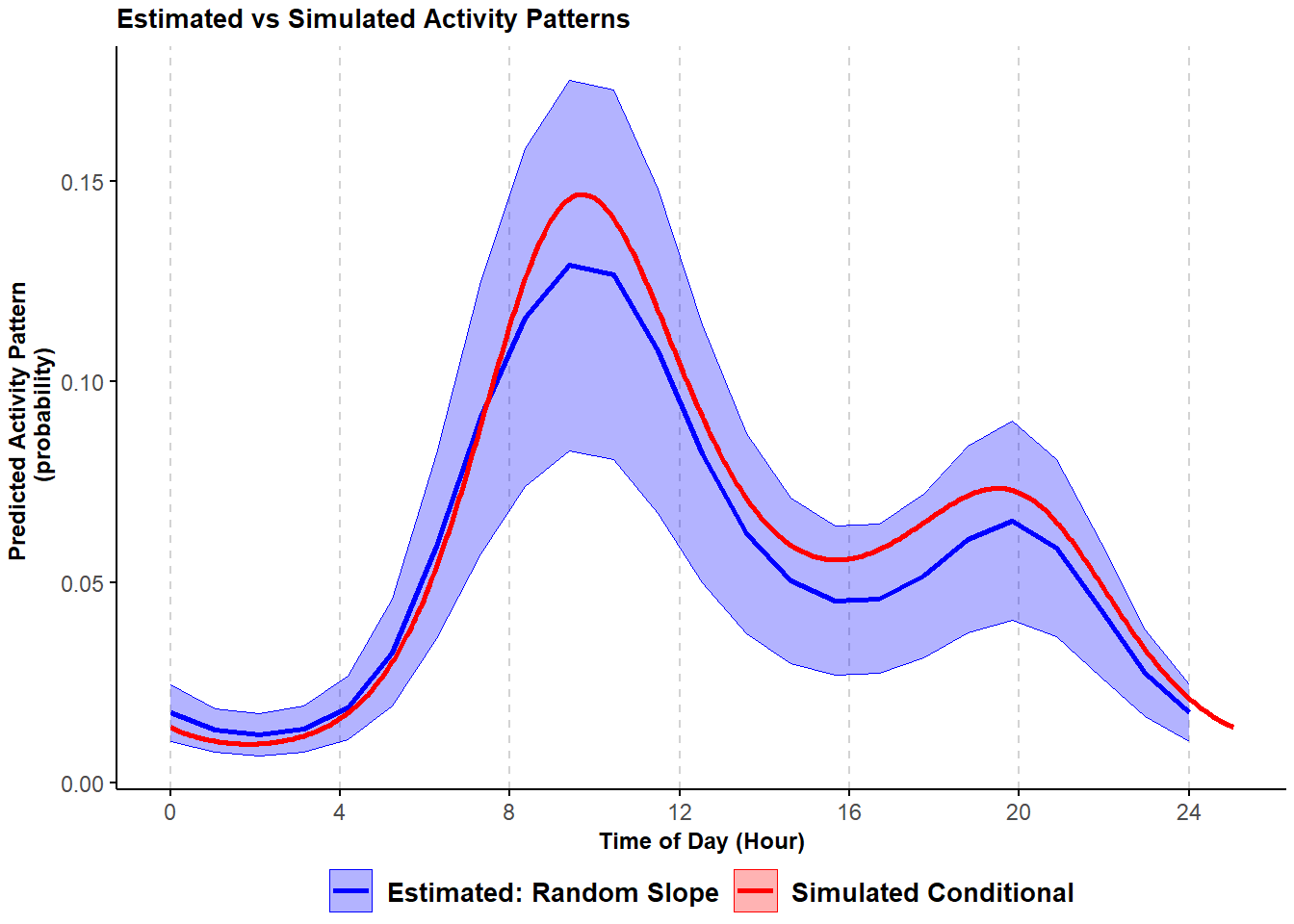

Figure 3.5: Comparison of simulated and HGAM estimated probability of activity conditional mean curves with variability in the frequency of site-use and timing of activity; shading corresponds to 95% confidence intervals.

Adding a component that allows for variability in timing of activity seems to improve the model fit and provides an estimated activity pattern that more closely resembles the one used to simulated the data.

Going forward. Throughout the tutorial, we fit trigonometric GLMMs using a binomial distribution (family = "binomial" in the code); however, we can run these models also using a Poisson distribution with a few adjustments to data and model structures. We report an example in section 10.2. When working with large datasets, using a Poisson distribution might result in lower computational times.

---

1. By allowing these terms to vary independently, we eliminate the need to estimate several covariance terms, which may be difficult with small numbers of sites.↩︎