Tutorial 8 Conditional and marginal mean activity patterns
GLMMs allow users to estimate both site-specific diel activity patterns and population-level activity patterns formed by averaging activity levels across sites in the population (see Box 1 in Iannarilli et al. (2024)). Site-specific estimates are frequently referred to as conditional means since they are formed by conditioning on a set of site-specific parameters; population-level means are often referred to as marginal means. Although one can estimate the conditional mean associated with any of the sampled sites, it is also common to plot the conditional mean for a ‘typical site’ (i.e. a site with average characteristics), formed by setting all of the random coefficients to their mean values (Fieberg et al. 2009).
Conditional and marginal mean activity patterns can be estimated in both the frequentist and Bayesian frameworks. The frequentist framework is generally accessible by more users than the Bayesian framework thanks to the availability of many ready-to-use R packages that implement GLMMs, so we first focus on this framework. An example of the same approach in the Bayesian framework is provided in section 10.3.
We use simulated data to illustrate how random intercept-only and random intercept and slope models are able to return differences in conditional and marginal mean activity patterns.
Data simulation. Using the approach introduced in Tutorials 2 and 3, we simulate encounter events for a species with a bimodal activity pattern using camera traps set at 100 sites with 30 days of sampling at each site. In addition to simulating the data, the sim_activity function also returns the ‘true’ conditional activity pattern for a typical site (one with random effects and ) at each of 513 equally spaced points between 0 and 24 hours (i.e. covering the diel activity pattern) using:
where , , , , and correspond to the parameter values used to simulate the data (see Tutorial 3).
In addition, the sim_activity function returns the ‘true’ marginal mean activity pattern, which is formed by averaging activity patterns across sites. To determine marginal means, we have to integrate over the distribution of the random effects:
Because this set of integrals has no closed-form solution, we must use approximation methods to solve for . In Tutorial 2, we used the integrate function to approximate . Alternatively, the sim_activity function estimates the marginal mean curve using a simulation approach in which it randomly selects 100,000 sites and their associated values of and , determines site-specific activity patterns for these sites on the probability scale, and then averages these site-specific activity patterns at each of the 513 reference points between 0 and 23 hours.
If we plot the estimated conditional and marginal mean activity curves (Figure 8.1), we see that for this set of parameter values, the two means have a similar shape. However, marginal mean is higher than the conditional mean, suggesting a higher level of overall activity when measured at the population level compared to the activity level at a typical site.
# Load libraries and function to simulate activity patterns
library(dplyr)
library(GLMMadaptive)
library(mgcv)
library(tidyr)
source("source_functions/sim_activity.R")
source("source_functions/sim_to_minute.R")
set.seed(129)
# Set equations' parameters
M = 100
J = 30
wavelength = 24
n_peak = 2
b0 = -3
b1 = 1
b2 = 0.7
theta0 = 3
theta1 = 2
sd_tau = 1
sd_gamma = 0.3
time <- seq(0, wavelength, wavelength/512)
dat <- sim_activity(M = M,
J = J,
wavelength = wavelength,
n_peak = n_peak,
n_sim = 1,
b0 = -3,
b0_constant = TRUE, # common intercept
tau_constant = FALSE,
sdtau = sd_tau, # ~site-specific intercept
b1 = b1,
b2 = b2, # amplitude of the cosine terms
theta0 = theta0,
theta1 = theta1, # common phaseshifts for the cosine terms
phaseshift_constant = FALSE,
sd_phaseshift = sd_gamma, # site-specific phaseshift (equal for both cosine terms)
plot_true_act = TRUE
)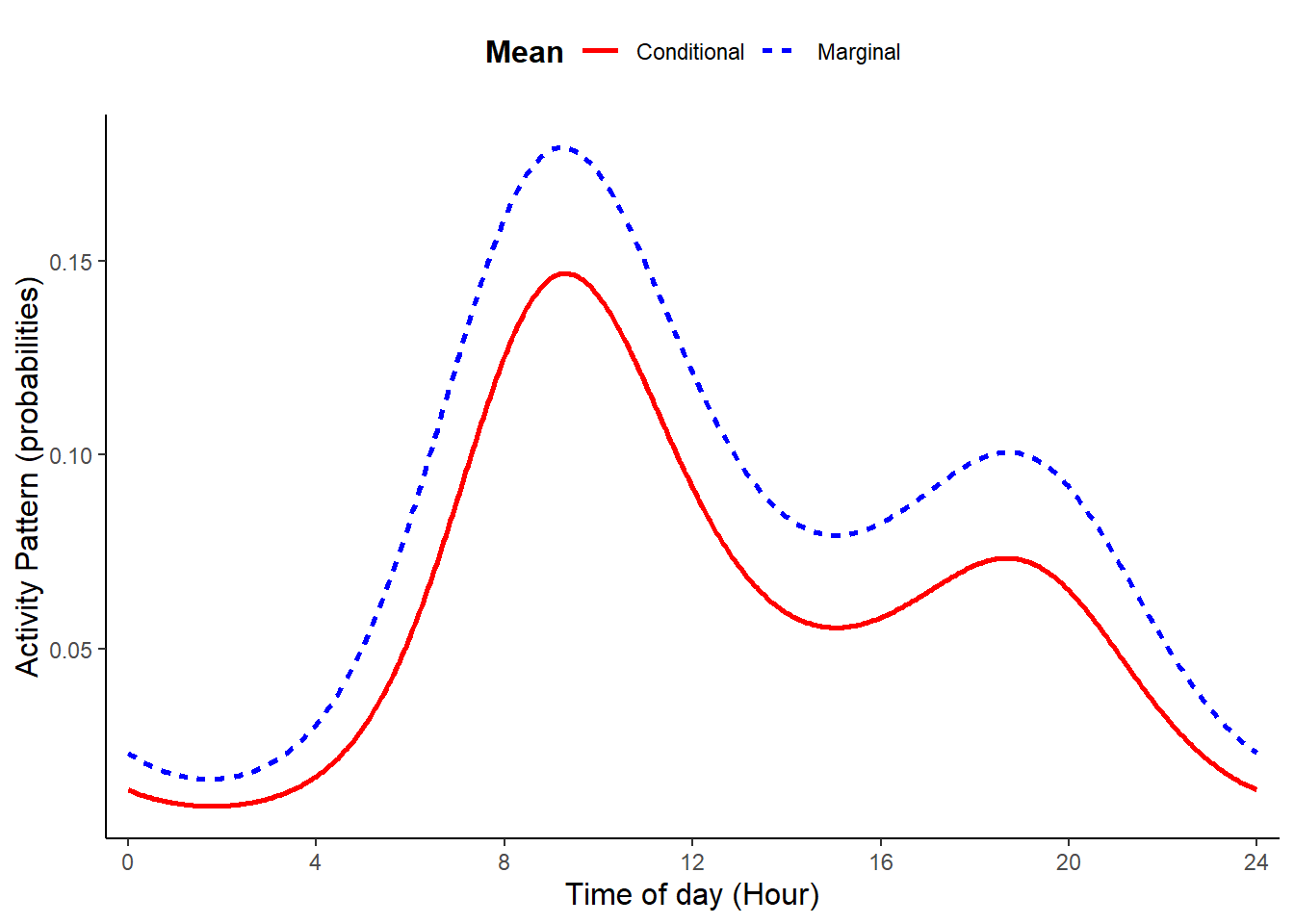
Figure 8.1: Conditional activity pattern for a typical site (one with random effects equal to zero) and marginal mean activity pattern formed by averaging site-specific activity patterns across a population of sites.
8.1 Estimating conditional and marginal mean activity patterns
Before fitting models, we need to prepare the data. We use the code from Tutorial 3 to aggregate the data by site, resulting in a data set with the following variables:
Site= ID for each surveyed siteTime= hour of daysuccess= number of encounters at the particularSiteandTimen_events= number of observation intervals associated with the particularSiteandTimefailure= number of observation intervals without an encounters at the particularSiteandTime
# The data
y <- as.data.frame(dat$sim_data)
# summarize aggregated data
y <- data.frame(id=paste("A", seq(1,M,1), sep=""),
y=as.data.frame(y)
)
colnames(y) <- c("id",
paste0("S", seq(1, ncol(y)-1, 1), sep="")
)
# Format data in long format
y_long <- pivot_longer(data = y, cols = -id, names_to = "time", values_to = "y") %>%
mutate(time=as.numeric(substr(time,2,10)),
id = factor(id)
)
# create variable to describe time as hour (between 0 and 23)
y_long$hour <- sim_to_minute(y_long$time, group = wavelength)
# count successes and failures at each site-occasion
occasions_cbind <- y_long %>%
group_by(id, hour) %>%
summarise(success = sum(y),
n_events = n(),
failure = n_events - success
) %>%
dplyr::rename(Site = id,
Time = hour
)## `summarise()` has grouped output by 'id'. You can override using the `.groups` argument.We are now ready to estimate conditional and marginal mean activity in the frequentist framework.
8.2 The frequentist framework
When using trigonometric GLMMs, we can quantify the conditional mean by setting all the random effects in the GLMM as equal to 0 and the marginal mean by integrating over the distribution of the random effects (Fieberg et al. 2009). Among the many packages available in R to model GLMMs, GLMMadaptive (Rizopoulos 2022) has the advantage of providing estimates of parameters describing both conditional and marginal mean response curves.
We start by fitting the model, similar to how we have done it in previous sections of these tutorials.
# Modelling activity pattern using trigonometric GLMMs in the parametric modelling framework
trig_rand_slope <- mixed_model(fixed = cbind(success, failure) ~
cos(2 * pi * Time/24) + sin(2 * pi * Time/24) +
cos(2 * pi * Time/12) + sin(2 * pi * Time/12),
random = ~ cos(2 * pi * Time/24) + sin(2 * pi * Time/24) +
cos(2 * pi * Time/12) + sin(2 * pi * Time/12) || Site,
data = occasions_cbind,
family = binomial(),
iter_EM = 0
)
summary(trig_rand_slope)##
## Call:
## mixed_model(fixed = cbind(success, failure) ~ cos(2 * pi * Time/24) +
## sin(2 * pi * Time/24) + cos(2 * pi * Time/12) + sin(2 * pi *
## Time/12), random = ~cos(2 * pi * Time/24) + sin(2 * pi *
## Time/24) + cos(2 * pi * Time/12) + sin(2 * pi * Time/12) ||
## Site, data = occasions_cbind, family = binomial(), iter_EM = 0)
##
## Data Descriptives:
## Number of Observations: 2400
## Number of Groups: 100
##
## Model:
## family: binomial
## link: logit
##
## Fit statistics:
## log.Lik AIC BIC
## -3704.187 7428.374 7454.425
##
## Random effects covariance matrix:
## StdDev
## (Intercept) 0.9742
## cos(2 * pi * Time/24) 0.0307
## sin(2 * pi * Time/24) 0.2343
## cos(2 * pi * Time/12) 0.1913
## sin(2 * pi * Time/12) 0.0430
##
## Fixed effects:
## Estimate Std.Err z-value p-value
## (Intercept) -3.0888 0.1000 -30.8945 < 1e-04
## cos(2 * pi * Time/24) -0.9410 0.0268 -35.1529 < 1e-04
## sin(2 * pi * Time/24) -0.1584 0.0345 -4.5927 < 1e-04
## cos(2 * pi * Time/12) -0.2659 0.0315 -8.4323 < 1e-04
## sin(2 * pi * Time/12) -0.5988 0.0237 -25.2223 < 1e-04
##
## Integration:
## method: adaptive Gauss-Hermite quadrature rule
## quadrature points: 7
##
## Optimization:
## method: quasi-Newton
## converged: TRUEIn most of the applications so far (except Tutorial 7), we explored the model results using the predicted conditional mean activity patterns. We calculated these patterns using the function effectPlotData, which is included in the GLMMadaptive package, by setting the argument marginal as equal FALSE. We do the same here. The conditional mean can be easily estimated using other packages available in R to fit GLMMs by setting the random effect equal to 0 and then predict the activity pattern over the 24-hour cycle. For example, we can use the predict function with the argument re.form = NA to obtain conditional means when models are fit using the glmer function in the lme4 package (Bates et al. 2015).
We can estimate marginal means using numerical integration (as done in Tutorial 2), simulation, or using various approximation methods (see e.g., section 19.2 of Fieberg 2024). The primary reason we explore mixed_model in the GLMMadaptive package is because it does the hard work for us. To calculate the predicted marginal mean activity pattern, we only need to change the argument marginal from FALSE to TRUE in the effectPlotData function.
newdat <- with(occasions_cbind,
expand.grid(Time = seq(min(Time), 24, length.out = 48))
)
cond_eff <- effectPlotData(trig_rand_slope, newdat, marginal = FALSE) %>%
mutate(pred = plogis(pred),
low = plogis(low),
upp = plogis(upp),
Method = "effectPlotData",
Mean = "Conditional"
)
marg_eff <- effectPlotData(trig_rand_slope, newdat, marginal = TRUE) %>%
mutate(pred = plogis(pred),
low = plogis(low),
upp = plogis(upp),
Method = "effectPlotData",
Mean = "Marginal"
)It is also possible to calculate both means using the estimated coefficients extracted directly from the fitted model. In this case, we can obtain estimates of the marginal coefficients that approximate the curve formed by integrating over the random effects using the marginal_coefs function in the GLMMadaptive package, which uses a numerical approximation based on an adaptive Gauss-Hermite quadrature rule (Hedeker et al. 2018) to calculate these values. From the parameter estimates, we can calculate the predicted conditional and marginal activity curves using the appropriate coefficient values along with the following equation:
betas <- matrix(c(t(GLMMadaptive::fixef(trig_rand_slope)),
t(GLMMadaptive::marginal_coefs(trig_rand_slope, std_errors = FALSE)$betas)
),
ncol=5, nrow = 2, byrow = TRUE
)
colnames(betas) <- colnames(t(GLMMadaptive::fixef(trig_rand_slope)))
rownames(betas) <- c("Conditional", "Marginal")
betas <- as.data.frame(betas) %>% dplyr::mutate(GLMM = "Rand_Intercept_and_Slope")
cond <- plogis(betas[1,1] +
betas[1,2] * cos(2*pi*time/24) +
betas[1,3] * sin(2*pi*time/24) +
betas[1,4] * cos(2*pi*time/12) +
betas[1,5] * sin(2*pi*time/12)
)
phat_cond <- data.frame(Time = time,
pred = cond,
low = NA,
upp = NA,
Method = "coeff. estimates",
Mean = "Conditional"
)
marg <- plogis(betas[2,1] +
betas[2,2] * cos(2*pi*time/24) +
betas[2,3] * sin(2*pi*time/24)+
betas[2,4] * cos(2*pi*time/12) +
betas[2,5] * sin(2*pi*time/12)
)
phat_marg <- data.frame(Time = time,
pred = marg,
low = NA,
upp = NA,
Method = "coeff. estimates",
Mean = "Marginal"
)We visually compare the estimates returned by both methods, and the two estimates to the true conditional and marginal activity patterns used to simulate the data.
# extract true conditional and marginal patterns
cond_true <- dat$Conditional %>%
mutate(low = NA,
upp = NA,
Method = "True pattern",
Mean = "Conditional") %>%
dplyr::rename(Time = time, pred = p) %>%
select(Time, pred, low, upp, Method, Mean)
marg_true <- dat$Marginal %>%
mutate(low = NA,
upp = NA,
Method = "True pattern",
Mean = "Marginal") %>%
dplyr::rename(Time = time, pred = p) %>%
select(Time, pred, low, upp, Method, Mean)
# bring all the information together in one dataset
res <- rbind(cond_true, marg_true, cond_eff, marg_eff, phat_cond, phat_marg)ggplot(res, aes(x = Time, y= pred, col = Method)) +
geom_ribbon(aes(ymin = low, ymax = upp, fill = Method), alpha = 0.1) +
geom_line(linewidth = 1) +
labs(x = "Time of Day (Hour)", y = "Activity Pattern \n (probability)")+
theme_minimal()+
theme(legend.position = "bottom",
legend.title = element_blank(),
legend.text = element_text(size=10,face="bold"),
legend.margin=margin(0,0,0,0),
legend.box.margin=margin(-5,-10,-10,-10),
plot.title = element_text(size=10,face="bold"),
axis.line = element_line(colour = 'black', linetype = 'solid'),
axis.ticks = element_line(colour = 'black', linetype = 'solid'),
axis.title = element_text(size=9,face="bold"),
panel.grid.minor.y = element_blank(),
panel.grid.major.y = element_blank(),
panel.grid.major.x = element_line(colour = 'lightgrey', linetype = 'dashed', linewidth=0.5),
panel.grid.minor.x = element_blank(),
strip.text = element_text(size = 9, colour = "black", face = "bold", hjust = 0),
plot.margin = margin(0.1,0.1,0.5,0.1, "cm")
) +
scale_x_continuous(breaks=seq(0,23,length.out=7), labels=seq(0,24,4)) +
facet_wrap(~Mean) ## Warning in max(ids, na.rm = TRUE): no non-missing arguments to max; returning -Inf
## Warning in max(ids, na.rm = TRUE): no non-missing arguments to max; returning -Inf
## Warning in max(ids, na.rm = TRUE): no non-missing arguments to max; returning -Inf
## Warning in max(ids, na.rm = TRUE): no non-missing arguments to max; returning -Inf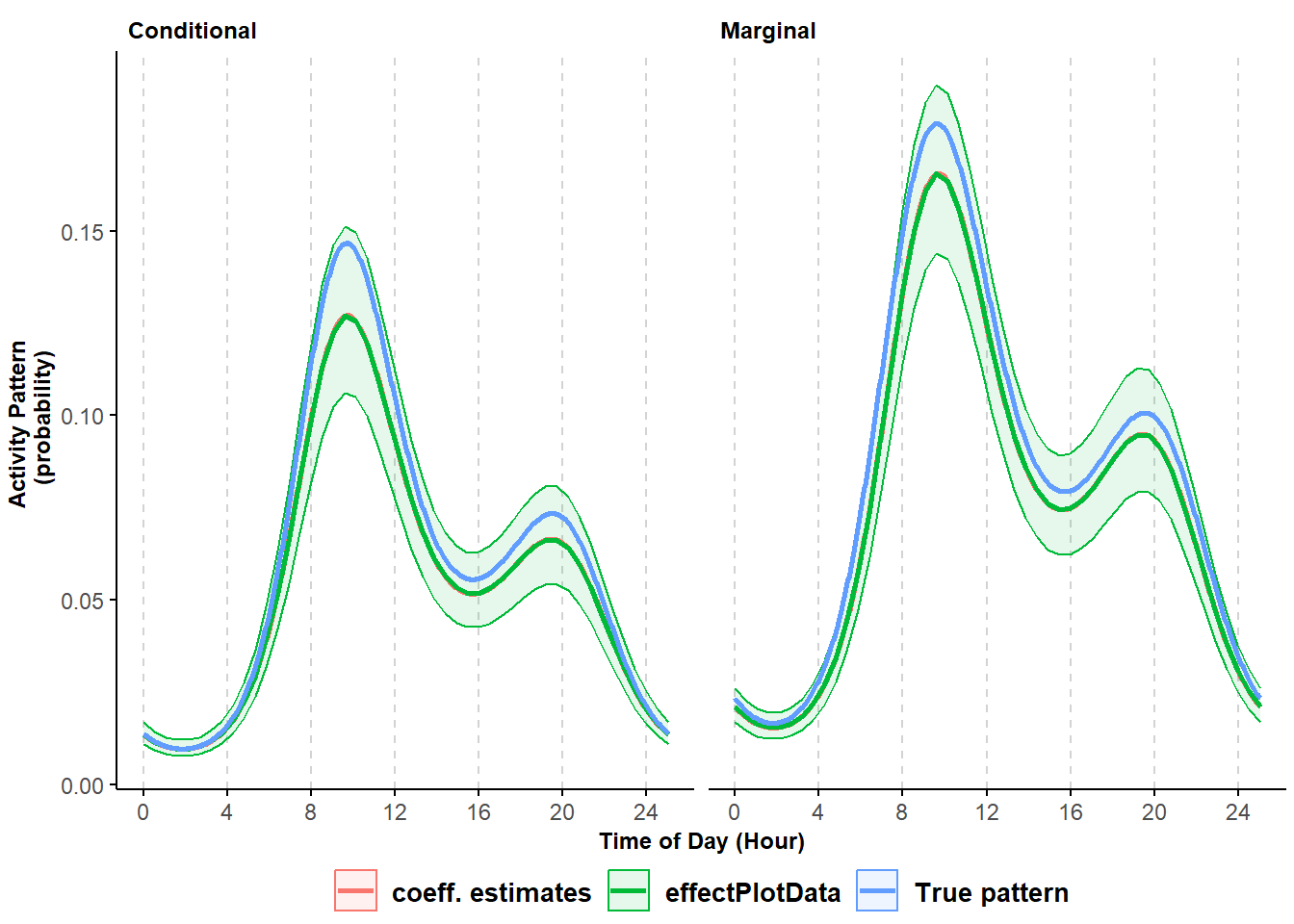
Figure 8.2: Comparison of marginal and conditional activity curves produced two ways along with true values used to simulate data.
The mean activity patterns returned by the effectDataPlot function and by the manual calculation match perfectly and both closely track the true, simulated conditional and marginal activity curves. The choice of which of the two predictive methods to use depends on the complexity of the fitted model. The effectDataPlot function can require long times to return a prediction when a random slope is included.